More about shock waves – normal and oblique shocks
Let us look once more at the nose of our supersonic aircraft. We saw how the shock waves formed in front of it, slowing the air down almost instantaneously and providing a subsonic patch through which the pressure information could propagate a limited distance upstream at the speed of sound (Fig. 5.2). It should be noted that the shock wave itself is able to make headway against the oncoming stream above the speed of sound. Only weak pressure disturbances travel at the speed of sound. The stronger the shock wave is, the faster it can travel through the air.
Considering the problem from the point of view of a stream of air approaching a stationary aircraft, this means that the faster the oncoming stream, the stronger the shock wave at the nose becomes. Thus the changes in pressure, density, temperature and velocity which occur through the shock wave all increase with increasing air speed upstream of the shock wave. A mathematical analysis of the problem shows that the strength of the shock wave, expressed as the ratio of the pressure in front of the wave to that behind, depends solely on the Mach number of the approaching air stream.
If we now stand further back from the aircraft we see that the bow shock wave which forms over the nose is, in fact, curved (Fig. 5.3(a)). As we get further from the nose tip so the shock wave becomes inclined to the direction of the oncoming flow. In this region the shock wave is said to be oblique. At the nose, where it is at right angles to the oncoming flow, it is said to be a normal shock wave.
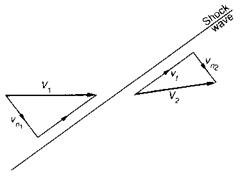
The oblique shock wave acts in the same way as the normal wave except that it only affects the component of velocity at right angles to itself. The component of velocity parallel to the wave is completely unaffected. This means that the direction of the flow is changed by an oblique shock (Fig. 5.6) whereas
|
Fig. 5.6 Flow deflection by oblique shock wave Tangential component Vt remains unchanged but V„2 < Vn |
|
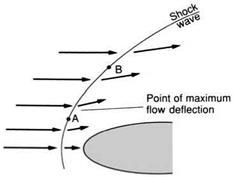
Fig. 5.7 Flow deflection through bow shock wave Deflection reaches a maximum and then reduces again |
it is unaffected by a normal shock. In both cases, however, the magnitude of the velocity is reduced as the flow passes through the shock wave.
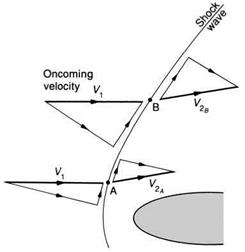
Looking more carefully at the effect of the bow shock wave (Fig. 5.7) we see that, in general, the same flow deflection can be obtained by two possible angles of oblique wave. The reason for this is given in Fig. 5.8. The wave of greater angle at A is stronger because the velocity component normal to the wave front is greater. It therefore changes the oncoming velocity component more than the weaker wave at point B.
Adding the resulting velocity components immediately downstream of the shock waves at two points (Fig. 5.8) shows how a particular point B (where the shock wave is weak) can be chosen with exactly the same flow deflection as at A (with a strong shock wave).
It should also be noted that for a normal shock wave the downstream flow is always subsonic, as it is for most strong oblique waves. The fact that the
|
Fig. 5.8 Weak and strong shock waves Strong shock at A gives same deflection as weak shock at B, but greater pressure jump since V2 < V2 |
velocity component parallel to the wave is not changed means, however, that the flow downstream of the weak oblique wave is supersonic.