Nonlifting Flow Over a Circular Cylinder

Consulting our road map given in Figure 3.4, we see that we are well into the third column, having already discussed uniform flow, sources and sinks, and doublets. Along the way, we have seen how the flow over a semi-infinite body can be simulated by the combination of a uniform flow with a source, and the flow over an oval-shaped body can be constructed by superimposing a uniform flow and a source-sink pair. In this section, we demonstrate that the combination of a uniform flow and a doublet produces the flow over a circular cylinder. A circular cylinder is one of the most

basic geometric shapes available, and the study of the flow around such a cylinder is a classic problem in aerodynamics.

Consider the addition of a uniform flow with velocity and a doublet of strength

к, as shown in Figure 3.26. The direction of the doublet is upstream, facing into the uniform flow. From Equations (3.57) and (3.87), the stream function for the combined flow is

l/r = УооГ sin в —

Let R2 = к/2nVoa. Then Equation (3.91) can be written as

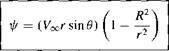[3.92]

Equation (3.92) is the stream function for a uniform flow-doublet combination; it is also the stream function for the flow over a circular cylinder of radius R as shown in Figure 3.26 and as demonstrated below.

The velocity field is obtained by differentiating Equation (3.92), as follows:

Figure 3.26 Superposition of a uniform flow and a doublet; nonlifting flow over a circular cylinder.

(V<xr sin0)—— + r*	(T^ sin 9)

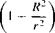
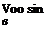
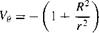[3.94]

To locate the stagnation points, set Equations (3.93) and (3.94) equal to zero:

[3.95]

[3.96]

Simultaneously solving Equations (3.95) and (3.96) for r and в, we find that there are two stagnation points, located at (г, в) = (R, 0) and (R, ж). These points are denoted as A and B, respectively, in Figure 3.26.

The equation of the streamline that passes through the stagnation point В is obtained by inserting the coordinates of В into Equation (3.92). For r = R and в = ж, Equation (3.92) yields r/r — 0. Similarly, inserting the coordinates of point A into Equation (3.92), we also find that = 0. Hence, the same streamline goes through both stagnation points. Moreover, the equation of this streamline, from Equation (3.92), is

Note that Equation (3.97) is satisfied by r = R for all values of 9. However, recall that R2 = к/2ж Уж, which is a constant. Moreover, in polar coordinates, r = constant = R is the equation of a circle of radius R with its center at the origin. Therefore, Equation (3.97) describes a circle with radius R, as shown in Figure 3.26. Moreover, Equation (3.97) is satisfied by в — ж and в — 0 for all values of r; hence, the entire horizontal axis through points A and B, extending infinitely far upstream and downstream, is part of the stagnation streamline.

Note that the [r — 0 streamline, since it goes through the stagnation points, is the dividing streamline. That is, all the flow inside xjr = 0 (inside the circle) comes from the doublet, and all the flow outside ij/ = 0 (outside the circle) comes from the uniform flow. Therefore, we can replace the flow inside the circle by a solid body, and the external flow will not know the difference. Consequently, the inviscid irrotational, incompressible flow over a circular cylinder of radius R can be synthesized by adding a uniform flow with velocity and a doublet of strength к, where R is related to Voo and к through

[3.98]

Note from Equations (3.92) to (3.94) that the entire flow field is symmetrical about both the horizontal and vertical axes through the center of the cylinder, as clearly seen by the streamline pattern sketched in Figure 3.26. Hence, the pressure

distribution is also symmetrical about both axes. As a result, the pressure distribution over the top of the cylinder is exactly balanced by the pressure distribution over the bottom of the cylinder (i. e., there is no net lift). Similarly, the pressure distribution over the front of the cylinder is exactly balanced by the pressure distribution over the back of the cylinder (i. e., there is no net drag). In real life, the result of zero lift is easy to accept, but the result of zero drag makes no sense. We know that any aerodynamic body immersed in a real flow will experience a drag. This paradox between the theoretical result of zero drag, and the knowledge that in real life the drag is finite, was encountered in the year 1744 by the Frenchman Jean Le Rond d’Alembert—and it has been known as d’Alembert’s paradox ever since. For d’Alembert and other fluid dynamic researchers during the eighteenth and nineteenth centuries, this paradox was unexplained and perplexing. Of course, today we know that the drag is due to viscous effects which generate frictional shear stress at the body surface and which cause the flow to separate from the surface on the back of the body, thus creating a large wake downstream of the body and destroying the symmetry of the flow about the vertical axis through the cylinder. These viscous effects are discussed in detail in Chapters 15 through 20. However, such viscous effects are not included in our present analysis of the inviscid flow over the cylinder. As a result, the inviscid theory predicts that the flow closes smoothly and completely behind the body, as sketched in Figure 3.26. It predicts no wake, and no asymmetries, resulting in the theoretical result of zero drag.

Let us quantify the above discussion. The velocity distribution on the surface of the cylinder is given by Equations (3.93) and (3.94) with r — R, resulting in

Note that at the surface of the cylinder, Vr is geometrically normal to the surface; hence, Equation (3.99) is consistent with the physical boundary condition that the component of velocity normal to a stationary solid surface must be zero. Equation (3.100) gives the tangential velocity, which is the full magnitude of velocity on the surface of the cylinder, that is, V = Vg = —2 V» sin 0 on the surface. The minus sign in Equation (3.100) is consistent with the sign convention in polar coordinates that Vg is positive in the direction of increasing в, that is, in the counterclockwise direction as shown in Figure 3.27. However, in Figure 3.26, the surface velocity for

Figure 3.27 Sign convention for

0 < в < jt is obviously in the opposite direction of increasing 0; hence, the minus sign in Equation (3.100) is proper. For it < 0 < In, the surface flow is in the same direction as increasing 0, but sin 0 is itself negative; hence, once again the minus sign in Equation (3.100) is proper. Note from Equation (3.100) that the velocity at the surface reaches a maximum value of 2Voo at the top and the bottom of the cylinder (where 0 = тг/2 and Зтг/2, respectively), as shown in Figure 3.28. Indeed, these are the points of maximum velocity for the entire flow field around the cylinder, as can be seen from Equations (3.93) and (3.94).

The pressure coefficient is given by Equation (3.38):

c„=,-(£)2 13.3.1

Cp = 1—4 sin[10] 0

Combining Equations (3.100) and (3.38), we find that the surface pressure coefficient over a circular cylinder is

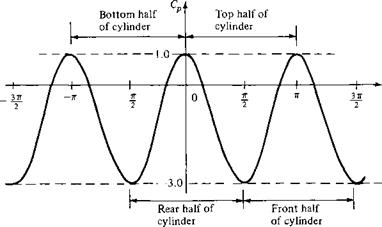
Note that Cp varies from 1.0 at the stagnation points to —3.0 at the points of maximum velocity. The pressure coefficient distribution over the surface is sketched in Figure 3.29. The regions corresponding to the top and bottom halves of the cylinder are identified at the top of Figure 3.29. Clearly, the pressure distribution over the top half of the cylinder is equal to the pressure distribution over the bottom half, and hence the lift must be zero, as discussed earlier. Moreover, the regions corresponding to the front and rear halves of the cylinder are identified at the bottom of Figure 3.29. Clearly, the pressure distributions over the front and rear halves are the same, and hence the drag is theoretically zero, as also discussed previously. These results are confirmed by Equations (1.15) and (1.16). Since Cf — 0 (we are dealing with an inviscid flow), Equations (1.15) and (1.16) become, respectively,

Figure 3.28

Pressure coefficient distribution over the surface of a circular cylinder; theoretical results for inviscid, incompressible flow.

Figure 3.29

For the circular cylinder, the chord c is the horizontal diameter. From Figure 3.29, Cp j = Cp u for corresponding stations measured along the chord, and hence the integrands in Equations (3.102) and (3.103) are identically zero, yielding cn = ca = 0. In turn, the lift and drag are zero, thus again confirming our previous conclusions.

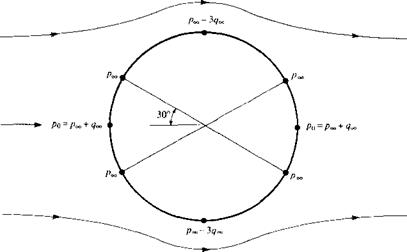
These points, as well as the stagnation points and points of minimum pressure, are illustrated in Figure 3.30. Note that at the stagnation point, where Cp = 1, the pressure is p^, + q-s. the pressure decreases to pco in the first 30° of expansion around the body, and the minimum pressure at the top and bottom of the cylinder, consistent with Cp = —3, is px — 3qca-

Values of pressure at various locations on the surface of a circular cylinder; nonlifting case.

Figure 3.30