Oblique Shock and Expansion Waves

In the case of air (and the same is true for all gases) the shock wave is extremely thin so that calculations based on one-dimensional flow are still applicable for determining the changes in velocity and density on passing through it, even when the rest of the flow system is not limited to one dimension, provided that only the velocity component normal to the wave is considered.

G. I. Taylor and J. W. Maccoll, 1934

9.1 Introduction

In Chapter 8, we discussed normal shock waves, that is, shock waves that make an angle of 90° with the upstream flow. The behavior of normal shock waves is important; moreover, the study of normal shock waves provides a relatively straightforward introduction to shock-wave phenomena. However, examining Figure 7.4a and the photographs shown in Figure 7.5, we see that, in general, a shock wave will make an oblique angle with respect to the upstream flow. These are called oblique shock waves and are the subject of part of this chapter. A normal shock wave is simply a special case of the general family of oblique shocks, namely, the case where the wave angle is 90°.

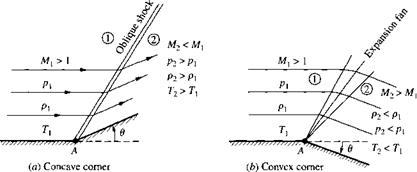
In addition to oblique shock waves, where the pressure increases discontinuously across the wave, supersonic flows are also characterized by oblique expansion waves, where the pressure decreases continuously across the wave. Let us examine these two types of waves further. Consider a supersonic flow over a wall with a corner at point A, as sketched in Figure 9.1. In Figure 9.1a, the wall is turned upward at the corner through the deflection angle в; that is, the corner is concave. The flow at the

Figure 9.1 Supersonic flow over a corner.

wall must be tangent to the wall; hence, the streamline at the wall is also deflected upward through the angle 9. The bulk of the gas is above the wall, and in Figure 9.1a, the streamlines are turned upward, into the main bulk of the flow. Whenever a supersonic flow is “turned into itself” as shown in Figure 9.1a, an oblique shock wave will occur. The originally horizontal streamlines ahead of the wave are uniformly deflected in crossing the wave, such that the streamlines behind the wave are parallel to each other and inclined upward at the deflection angle 9. Across the wave, the Mach number discontinuously decreases, and the pressure, density, and temperature discontinuously increase. In contrast, Figure 9.1 b shows the case where the wall is turned downward at the comer through the deflection angle 9; that is, the comer is convex. Again, the flow at the wall must be tangent to the wall; hence, the streamline at the wall is deflected downward through the angle 9. The bulk of the gas is above the wall, and in Figure 9.1 b, the streamlines are turned downward, away from the main bulk of the flow. Whenever a supersonic flow is “turned away from itself” as shown in Figure 9.1 b, an expansion wave will occur. This expansion wave is in the shape of a fan centered at the comer. The fan continuously opens in the direction away from the comer, as shown in Figure 9.1 b. The originally horizontal streamlines ahead of the expansion wave are deflected smoothly and continuously through the expansion fan such that the streamlines behind the wave are parallel to each other and inclined downward at the deflection angle 9. Across the expansion wave, the Mach number increases, and the pressure, temperature, and density decrease. Flence, an expansion wave is the direct antithesis of a shock wave.

Oblique shock and expansion waves are prevalent in two – and three-dimensional supersonic flows. These waves are inherently two-dimensional in nature, in contrast to the one-dimensional normal shock waves discussed in Chapter 8. That is, in Figure 9.1a and b, the flow-field properties are a function of x and y. The purpose of the present chapter is to determine and study the properties of these oblique waves.

What is the physical mechanism that creates waves in a supersonic flow? To ad­dress this question, recall our picture of the propagation of a sound wave via molecular collisions, as portrayed in Section 8.3. If a slight disturbance takes place at some point

in a gas, information is transmitted to other points in the gas by sound waves which propagate in all directions away from the source of the disturbance. Now consider a body in a flow, as sketched in Figure 9.2. The gas molecules which impact the body surface experience a change in momentum. In turn, this change is transmitted to neighboring molecules by random molecular collisions. In this fashion, information about the presence of the body attempts to be transmitted to the surrounding flow via molecular collisions; that is, the information is propagated upstream at approxi­mately the local speed of sound. If the upstream flow is subsonic, as shown in Figure 9.2a, the disturbances have no problem working their way far upstream, thus giving the incoming flow plenty of time to move out of the way of the body. On the other hand, if the upstream flow is supersonic, as shown in Figure 9.2b, the disturbances cannot work their way upstream; rather, at some finite distance from the body, the

Figure 9.2 Propagation of disturbances, (a) Subsonic flow, (b) Supersonic flow.

disturbance waves pile up and coalesce, forming a standing wave in front of the body. Hence, the physical generation of waves in a supersonic flow—both shock and ex­pansion waves—is due to the propagation of information via molecular collisions and due to the fact that such propagation cannot work its way into certain regions of the supersonic flow.

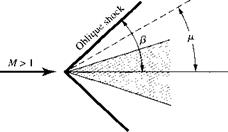
Why are most waves oblique rather than normal to the upstream flow? To answer this question, consider a small source of disturbance moving through a stagnant gas. For lack of anything better, let us call this disturbance source a “beeper,” which periodically emits sound. First, consider the beeper moving at subsonic speed through the gas, as shown in Figure 9.3a. The speed of the beeper is V, where V < a. At time t = 0, the beeper is located at point A; at this point, it emits a sound wave which propagates in all directions at the speed of sound, a. At a later time t this sound wave has propagated a distance at from point A and is represented by the circle of radius at shown in Figure 9.3a. During the same time, the beeper has moved a distance Vt and is now at point В in Figure 9.3a. Moreover, during its transit from A to B, the beeper has emitted several other sound waves, which at time t are represented by the smaller circles in Figure 9.3a. Note that the beeper always stays inside the family of circular sound waves and that the waves continuously move ahead of the beeper. This is because the beeper is traveling at a subsonic speed V < a. In contrast, consider the beeper moving at a supersonic speed V > a through the gas, as shown in Figure 9.3b. At time t = 0, the beeper is located at point A, where it emits a sound wave. At a later time t this sound wave has propagated a distance at from point A and is represented by the circle of radius at shown in Figure 9.3b. During the same time, the beeper has moved a distance V t to point B. Moreover, during its transit from A to B, the beeper has emitted several other sound waves, which at time t are represented by the smaller circles in Figure 9.3b. However, in contrast to the subsonic case, the beeper is now

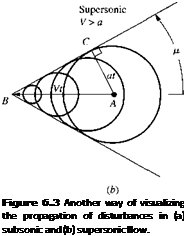constantly outside the family of circular sound waves; that is, it is moving ahead of the wave fronts because V > a. Moreover, something new is happening; these wave fronts form a disturbance envelope given by the straight line BC, which is tangent to the family of circles. This line of disturbances is defined as a Mach wave. In addition, the angle A BC which is the Mach wave makes with respect to the direction of motion of the beeper is defined as the Mach angle /л. From the geometry of Figure 9.3b, we readily find that

at

sin a — — lft

Thus, the Mach angle is simply determined by the local Mach number as

Examining Figure 93b, the Mach wave, that is, the envelope of disturbances in the supersonic flow, is clearly oblique to the direction of motion. If the disturbances are stronger than a simple sound wave, then the wave front becomes stronger than a Mach wave, creating an oblique shock wave at an angle /3 to the freestream, where fi > fi. This comparison is shown in Figure 9.4. However, the physical mechanism creating the oblique shock is essentially the same as that described above for the Mach wave. Indeed, a Mach wave is a limiting case for oblique shock (i. e., it is an infinitely weak oblique shock).

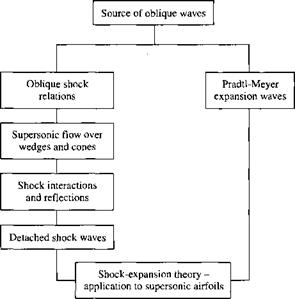
This finishes our discussion of the physical source of oblique waves in a super­sonic flow. Let us now proceed to develop the equations which allow us to calculate the change in properties across these oblique waves, first for oblique shock waves, and then for expansion waves. In the process, we follow the road map given in Figure

9.5.

Figure 9.4 Relation between the oblique shock-wave angle and the Mach angle.

Figure 0.5 Road map for Chapter 9.