Physical principle Energy can be neither created nor destroyed; it can only change in form

This physical principle is embodied in the first law of thermodynamics. A brief review of thermodynamics is given in Chapter 7. Thermodynamics is essential to the study of compressible flow; however, at this stage, we will only introduce the first law, and we defer any substantial discussion of thermodynamics until Chapter 7, where we begin to concentrate on compressible flow.

Consider a fixed amount of matter contained within a closed boundary. This matter defines the system. Because the molecules and atoms within the system are constantly in motion, the system contains a certain amount of energy. For simplicity, let the system contain a unit mass; in turn, denote the internal energy per unit mass by e.

The region outside the system defines the surroundings. Let an incremental amount of heat 8q be added to the system from the surroundings. Also, let 8w be the work done on the system by the surroundings. (The quantities 8q and 8w are discussed in more detail in Chapter 7.) Both heat and work are forms of energy, and when added to the system, they change the amount of internal energy in the system. Denote this change of internal energy by de. From our physical principle that energy is conserved, we have for the system

8q + 8w = de [2.85]

Equation (2.85) is a statement of the first law of thermodynamics.

Let us apply the first law to the fluid flowing through the fixed control volume shown in Figure 2.17. Let

B = rate of heat added to fluid inside control volume from surroundings

Z?2 = rate of work done on fluid inside control volume

Вт, = rate of change of energy of fluid as it flows through control volume

From the first law,

Note that each term in Equation (2.86) involves the time rate of energy change; hence, Equation (2.86) is, strictly speaking, a power equation. However, because it is a statement of the fundamental principle of conservation of energy, the equation is conventionally termed the “energy equation.” We continue this convention here.

First, consider the rate of heat transferred to or from the fluid. This can be visual­ized as volumetric heating of the fluid inside the control volume due to absorption of radiation originating outside the system or the local emission of radiation by the fluid itself, if the temperature inside the control volume is high enough. In addition, there may be chemical combustion processes taking place inside the control volume, such as fuel-air combustion in a jet engine. Let this volumetric rate of heat addition per unit mass be denoted by q. Typical units for q are J/s • kg or ft • lb/s • slug. Examining Figure 2.17, the mass contained within an elemental volume is p dV hence, the rate of heat addition to this mass is q{p dV). Summing over the complete control volume, we obtain

In addition, if the flow is viscous, heat can be transferred into the control volume by means of thermal conduction and mass diffusion across the control surface. At this stage, a detailed development of these viscous heat-addition terms is not warranted; they are considered in detail in Chapter 15. Rather, let us denote the rate of heat addition to the control volume due to viscous effects simply by Qviscous – Therefore, in Equation (2.86), the total rate of heat addition is given by Equation (2.87) plus

Q viscous*

[2.88]

в 1

V

Before considering the rate of work done on the fluid inside the control volume, consider a simpler case of a solid object in motion, with a force F being exerted on the object, as sketched in Figure 2.23. The position of the object is measured from a fixed origin by the radius vector r. In moving from position Г] to Г2 over an interval

Later time, t + dt

Figure 2.23 Schematic for the rate of doing work by a force F exerted on a moving body.

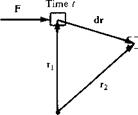
of time dt, the object is displaced through dr. By definition, the work done on the object in time dt is F • dr. Hence, the time rate of doing work is simply F • йт/dt. However, йт/dt = V, the velocity of the moving object. Hence, we can state that

Rate of doing work on moving body = F • V

In words, the rate of work done on a moving body is equal to the product of its velocity and the component of force in the direction of the velocity.

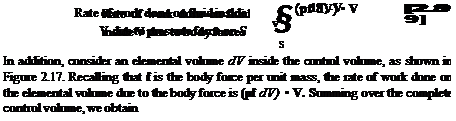This result leads to an expression for B2, as follows. Consider the elemental area dS of the control surface in Figure 2.17. The pressure force on this elemental area is —p dS. From the above result, the rate of work done on the fluid passing through dS with velocity V is (—p dS) • V. Hence, summing over the complete control surface, we have

If the flow is viscous, the shear stress on the control surface will also perform work on the fluid as it passes across the surface. Once again, a detailed development of this term is deferred until Chapter 15. Let us denote this contribution simply by VTViSCOUS. Then the total rate of work done on the fluid inside the control volume is the sum of Equations (2.89) and (2.90) and VTviscou

+

S V

To visualize the energy inside the control volume, recall that in the first law of thermodynamics as stated in Equation (2.85), the internal energy e is due to the random motion of the atoms and molecules inside the system. Equation (2.85) is written for a stationary system. However, the fluid inside the control volume in Figure 2.17 is not stationary; it is moving at the local velocity V with a consequent kinetic energy per unit mass of Vі/2. Hence, the energy per unit mass of the moving fluid is the sum of both internal and kinetic energies e + Vі/2. This sum is called the total energy per unit mass.

We are now ready to obtain an expression for ZL, the rate of change of total energy of the fluid as it flows through the control volume. Keep in mind that mass flows into the control volume of Figure 2.17 bringing with it a certain total energy; at the same time mass flows out of the control volume taking with it a generally different amount of total energy. The elemental mass flow across dS is pV • dS, and therefore

the elemental flow of total energy across dS is (pV • dS)(e + V2/2). Summing over the complete control surface, we obtain

In addition, if the flow is unsteady, there is a time rate of change of total energy inside the control volume due to the transient fluctuations of the flow-field variables. The total energy contained in the elemental volume dV is p(<? + V2/2) dV, and hence the total energy inside the complete control volume at any instant in time is

Therefore,

Time rate of change of total energy
inside V due to transient variations
of flow-field variables

In turn, S3 is the sum of Equations (2.92)

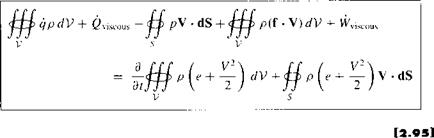Repeating the physical principle stated at the beginning of this section, the rate of heat added to the fluid plus the rate of work done on the fluid is equal to the rate of change of total energy of the fluid as it flows through the control volume; i. e., energy is conserved. In turn, these words can be directly translated into an equation by combining Equations (2.86), (2.88), (2.91), and (2.94):

Equation (2.95) is the energy equation in integral form; it is essentially the first law of thermodynamics applied to a fluid flow.

For the sake of completeness, note that if a shaft penetrates the control surface in Figure 2.17, driving some power machinery located inside the control volume (say, a compressor of a jet engine), then the rate of work delivered by the shaft, lVShafb must be added to the left side of Equation (2.95). Also note that the potential energy does not appear explicitly in Equation (2.95). Changes in potential energy are contained in the body force term when the force of gravity is included in f. For the aerodynamic

problems considered in this book, shaft work is not treated, and changes in potential energy are always negligible.

Following the approach established in Sections 2.4 and 2.5, we can obtain a partial differential equation for total energy from the integral form given in Equation

(2.95) . Applying the divergence theorem to the surface integrals in Equation (2.95), collecting all terms inside the same volume integral, and setting the integrand equal to zero, we obtain

3	Г ( v2X		г / v2 1
dt	/Т + т)_	+ V.	4c+t)v	= pq-V • (p) + p(f ■ V)
				+ &. + w!- 1 ^ VISCOUS 1 VISCOUS

[2.96]

where <2viscous and ^viscous represent the proper forms of the viscous terms, to be obtained in Chapter 15. Equation (2.96) is a partial differential equation which relates the flow-field variables at a given point in space.

If the flow is steady (3/31 = 0), inviscid ((/viscous = 0 and Wviscous = 0), adiabatic (no heat addition, q = 0), without body forces (f = 0), then Equations

(2.95) aEquations (2.97) and (2.98) are discussed and applied at length beginning with Chapter 7.

With the energy equation, we have introduced another unknown flow-field vari­able e. We now have three equations, continuity, momentum, and energy, which involve four dependent variables, p, p, V, and e. A fourth equation can be obtained from a thermodynamic state relation for e (see Chapter 7). If the gas is calorically perfect, then

e = cvT [2.99]

where cv is the specific heat at constant volume. Equation (2.99) introduces temper­ature as yet another dependent variable. However, the system can be completed by using the perfect gas equation of state

p — pRT [2.100]

where R is the specific gas constant. Therefore, the continuity, momentum, and energy equations, along with Equations (2.99) and (2.100) are five independent equations

for the five unknowns, p p, V, e, and T. The matter of a perfect gas and related equations of state are reviewed in detail in Chapter 7; Equations (2.99) and (2.100) are presented here only to round out our development of the fundamental equations of fluid flow.