Physical principle Mass can be neither created nor destroyed

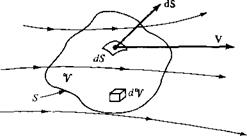
Consider a flow field wherein all properties vary with spatial location and time, e. g., p — p(x, y,z, t). In this flow field, consider the fixed finite control volume shown in Figure 2.17. At a point on the control surface, the flow velocity is V and the vector elemental surface area is dS. Also dV is an elemental volume inside the control volume. Applied to this control volume, the above physical principle means

Net mass flow out of control _ time rate of decrease of volume through surface S mass inside control volume V

or В = C where В and C are just convenient symbols for the left and right sides, respectively, of Equation (2.45a). First, let us obtain an expression for В in terms of the quantities shown in Figure 2.17. From Equation (2.43), the elemental mass flow across the area dS is

pVn dS = p • dS

Examining Figure 2.17, note that by convention, dS always points in a direction out of the control volume. Hence, when V also points out of the control volume (as shown

Figure 2.1 7 Finite control volume fixed in space.

in Figure 2.17), the product pV • dS is positive. Moreover, when V points out of the control volume, the mass flow is physically leaving the control volume; i. e., it is an outflow. Hence, a positive pV • dS denotes an outflow. In turn, when V points into the control volume, pV • dS is negative. Moreover, when V points inward, the mass flow is physically entering the control volume; i. e., it is an inflow. Hence, a negative pV • dS denotes an inflow. The net mass flow out of the entire control surface S is the summation over S of the elemental mass flows. In the limit, this becomes a surface integral, which is physically the left side of Equations (2.45a and b) i. e.,

physical principle of the conservation of mass to a finite control volume fixed in space. Equation (2.48) is called the continuity equation. It is one of the most fundamental equations of fluid dynamics.

Note that Equation (2.48) expresses the continuity equation in integral form. We will have numerous opportunities to use this form; it has the advantage of relating aerodynamic phenomena over a finite region of space without being concerned about the details of precisely what is happening at a given distinct point in the flow. On the other hand, there are many times when we are concerned with the details of a flow and we want to have equations that relate flow properties at a given point. In such a case, the integral form as expressed in Equation (2.48) is not particularly useful. However, Equation (2.48) can be reduced to another form that does relate flow properties at a given point, as follows. To begin with, since the control volume used to obtain Equation (2.48) is fixed in space, the limits of integration are also fixed. Hence, the time derivative can be placed inside the volume integral and Equation (2.48) can be written as

[2.49]

Applying the divergence theorem, Equation (2.26), we can express the right-hand term of Equation (2.49) as

Substituting Equation (2.50) into (2.49), we obtain

Examine the integrand of Equation (2.51). If the integrand were a finite number, then Equation (2.51) would require that the integral over part of the control volume be equal and opposite in sign to the integral over the remainder of the control volume, such that the net integration would be zero. However, the finite control volume is arbitrarily drawn in space; there is no reason to expect cancellation of one region by the other. Hence, the only way for the integral in Equation (2.51) to be zero for an

arbitrary control volume is for the integrand to be zero at all points within the control volume. Thus, from Equation (2.51), we have

Equation (2.52) is the continuity equation in the form of a partial differential equation. This equation relates the flow field variables at a point in the flow, as opposed to Equation (2.48), which deals with a finite space.

It is important to keep in mind that Equations (2.48) and (2.52) are equally valid statements of the physical principle of conservation of mass. They are mathematical representations, but always remember that they speak words—they say that mass can be neither created nor destroyed.

Note that in the derivation of the above equations, the only assumption about the nature of the fluid is that it is a continuum. Therefore, Equations (2.48) and (2.52) hold in general for the three-dimensional, unsteady flow of any type of fluid, inviscid or viscous, compressible or incompressible. (Note: It is important to keep track of all assumptions that are used in the derivation of any equation because they tell you the limitations on the final result, and therefore prevent you from using an equation for a situation in which it is not valid. In all our future derivations, develop the habit of noting all assumptions that go with the resulting equations.)

It is important to emphasize the difference between unsteady and steady flows. In an unsteady flow, the flow-field variables are a function of both spatial location and time, e. g.,

P – P(x, У, z, t)

This means that if you lock your eyes on one fixed point in space, the density at that point will change with time. Such unsteady fluctuations can be caused by time – varying boundaries (e. g., an airfoil pitching up and down with time or the supply valves of a wind tunnel being turned off and on). Equations (2.48) and (2.52) hold for such unsteady flows. On the other hand, the vast majority of practical aerodynamic problems involve steady flow. Here, the flow-field variables are a function of spatial location only, e. g.,

P = P(x, y, z)