Physical Significance
Consider again the basic model underlying Prandtl’s lifting-line theory. Return to Figure 5.13 and study it carefully. An infinite number of infinitesimally weak horseshoe vortices are superimposed in such a fashion as to generate a lifting line which spans the wing, along with a vortex sheet which trails downstream. This trailing-vortex sheet is the instrument that induces downwash at the lifting line. At first thought, you might consider this model to be somewhat abstract—a mathematical convenience that somehow produces surprisingly useful results. However, to the contrary, the model shown in Figure 5.13 has real physical significance. To see this more clearly, return to Figure 5.1. Note that in the three-dimensional flow over a finite wing, the streamlines leaving the trailing edge from the top and bottom surfaces are in different directions; that is, there is a discontinuity in the tangential velocity at the trailing edge. We know from Chapter 4 that a discontinuous change in tangential velocity is theoretically allowed across a vortex sheet. In real life, such discontinuities do not exist; rather, the different velocities at the trailing edge generate a thin region of large velocity gradients—a thin region of shear flow with very large vorticity. Hence, a sheet of vorticity actually trails downstream from the trailing edge of a finite wing. This sheet
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 Consider a rectangular wing with an aspect ratio of 6, an induced drag factor 5 = 0.055, and a zero-lift angle of attack of —2°. At an angle of attack of 3.4°, the induced drag coefficient for this wing is 0.01. Calculate the induced drag coefficient for a similar wing (a rectangular wing with the same airfoil section) at the same angle of attack, but with an aspect ratio of 10. Assume that the induced factors for drag and the lift slope, S and r, respectively, are equal to each other (i. e., 5 = г). Also, for AR = 10, 5 = 0.105.
Consider a rectangular wing with an aspect ratio of 6, an induced drag factor 5 = 0.055, and a zero-lift angle of attack of —2°. At an angle of attack of 3.4°, the induced drag coefficient for this wing is 0.01. Calculate the induced drag coefficient for a similar wing (a rectangular wing with the same airfoil section) at the same angle of attack, but with an aspect ratio of 10. Assume that the induced factors for drag and the lift slope, S and r, respectively, are equal to each other (i. e., 5 = г). Also, for AR = 10, 5 = 0.105.
Solution
We must recall that although the angle of attack is the same for the two cases compared here (AR = 6 and 10), the value of Cl is different because of the aspect-ratio effect on the lift slope. First, let us calculate Cl for the wing with aspect ratio 6. From Equation (5.61),
Hence, CL = 0.423
The lift slope of this wing is therefore dCL 0.423
—– = —————- = 0.078/degree = 4.485/rad
da 3.4° – (-2°) ‘ 6 ‘
![]()
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||

Note: This problem would have been more straightforward if the lift coefficients had been stipulated to be the same between the two wings rather than the angle of attack. Then Equation (5.61) would have yielded the induced drag coefficient directly. A purpose of this example is to reinforce the rationale behind Equation (5.65), which readily allows the scaling of drag coefficients from one aspect ratio to another, as long as the lift coefficient is the same. This allows the scaled drag-coefficient data to be plotted versus CL (not the angle of attack) as in Figure 5.20. However, in the present example where the angle of attack is the same between both cases, the effect of aspect ratio on the lift slope must be explicitly considered, as we have done above.
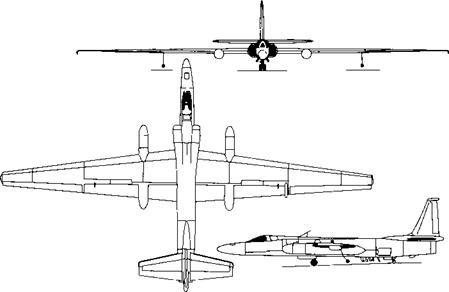
 Consider the twin-jet executive transport discussed in Example 1.6. In addition to the information given in Example 1.6, for this airplane the zero-lift angle of attack is —2°, the lift slope of the airfoil section is 0.1 per degree, the lift efficiency factor r = 0.04, and the wing aspect ratio is 7.96. At the cruising condition treated in Example 1.6, calculate the angle of attack of the airplane.
Consider the twin-jet executive transport discussed in Example 1.6. In addition to the information given in Example 1.6, for this airplane the zero-lift angle of attack is —2°, the lift slope of the airfoil section is 0.1 per degree, the lift efficiency factor r = 0.04, and the wing aspect ratio is 7.96. At the cruising condition treated in Example 1.6, calculate the angle of attack of the airplane.
Solution
The lift slope of the airfoil section in radians is
a0 = 0.1 per degree = 0.1 (57.3) = 5.73 rad From Equation (5.70) repeated below
_ _____ "o____
1 + (a0/7rAR)(l + r)
![]()
|
|
|
|
|
|
![]()













