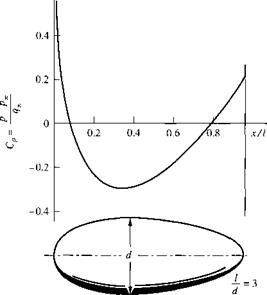
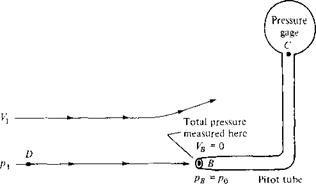
Pitot Tube: Measurement of Airspeed

In 1732, the Frenchman Henri Pitot was busy trying to measure the flow velocity of the Seine River in Paris. One of the instruments he used was his own invention—a strange-looking tube bent into an L shape, as shown in Figure 3.11. Pitot oriented one of the open ends of the tube so that it faced directly into the flow. In turn, he used the pressure inside this tube to measure the water flow velocity. This was the first time in history that a proper measurement of fluid velocity was made, and Pitot’s invention has carried through to the present day as the Pitot tube—one of the most common and frequently used instruments in any modern aerodynamic laboratory. Moreover, a Pitot tube is the most common device for measuring flight velocities of airplanes. The purpose of this section is to describe the basic principle of the Pitot tube.5

Consider a flow with pressure p moving with velocity V. as sketched at the left of Figure 3.11. Let us consider the significance of the pressure p more closely. In Section 1.4, the pressure is associated with the time rate of change of momentum of the gas molecules impacting on or crossing a surface; that is, pressure is clearly related to the motion of the molecules. This motion is very random, with molecules moving in all directions with various velocities. Now imagine that you hop on a fluid

5 See chapter 4 of Reference 2 for a detailed discussion of the history of the Pitot tube, how Pitot used it to overturn о basic theory in civil engineering, how it created some controversy in engineering, and how it finally found application in aeronautics.

Static pressure A /measured here

yy>//777;77^ " 7^7777777^

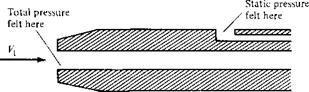
Figure 3.1 1 Pitot tube and a static pressure orifice.

element of the flow and ride with it at the velocity V. The gas molecules, because of their random motion, will still bump into you, and you will feel the pressure p of the gas. We now give this pressure a specific name: the static pressure. Static pressure is a measure of the purely random motion of molecules in the gas; it is the pressure you feel when you ride along with the gas at the local flow velocity. All pressures used in this book so far have been static pressures; the pressure p appearing in all our previous equations has been the static pressure. In engineering, whenever a reference is made to “pressure” without further qualification, that pressure is always interpreted as the static pressure. Furthermore, consider a boundary of the flow, such as a wall, where a small hole is drilled perpendicular to the surface. The plane of the hole is parallel to the flow, as shown at point A in Figure 3.11. Because the flow moves over the opening, the pressure felt at point A is due only to the random motion of the molecules; that is, at point A, the static pressure is measured. Such a small hole in the surface is called a static pressure orifice, or a static pressure tap.

In contrast, consider that a Pitot tube is now inserted into the flow, with an open end facing directly into the flow. That is, the plane of the opening of the tube is perpendicular to the flow, as shown at point В in Figure 3.11. The other end of the Pitot tube is connected to a pressure gage, such as point C in Figure 3.11 (i. e., the Pitot tube is closed at point C). For the first few milliseconds after the Pitot tube is inserted into the flow, the gas will rush into the open end and will fill the tube. However, the tube is closed at point C; there is no place for the gas to go, and hence after a brief period of adjustment, the gas inside the tube will stagnate; that is, the gas velocity inside the tube will go to zero. Indeed, the gas will eventually pile up

and stagnate everywhere inside the tube, including at the open mouth at point B. As a result, the streamline of the flow that impinges directly at the open face of the tube (streamline DB in Figure 3.11) sees this face as an obstruction to the flow. The fluid elements along streamline DB slow down as they get closer to the Pitot tube and go to zero velocity right at point B. Any point in a flow where V = 0 is called a stagnation point of the flow; hence, point В at the open face of the Pitot tube is a stagnation point, where VB = 0. In turn, from Bernoulli’s equation we know the pressure increases as the velocity decreases. Hence, pB > p. The pressure at a stagnation point is called the stagnation pressure, or total pressure, denoted by po- Hence, at point В, рв = po-

From the above discussion, we see that two types of pressure can be defined for a given flow: static pressure, which is the pressure you feel by moving with the flow at its local velocity Vj, and total pressure, which is the pressure that the flow achieves when the velocity is reduced to zero. In aerodynamics, the distinction between total and static pressure is important; we have discussed this distinction at some length, and you should make yourself comfortable with the above paragraphs before proceeding further. (Further elaboration on the meaning and significance of total and static pressure will be made in Chapter 7.)

How is the Pitot tube used to measure flow velocity? To answer this question, first note that the total pressure po exerted by the flow at the tube inlet (point В) is impressed throughout the tube (there is no flow inside the tube; hence, the pressure everywhere inside the tube is po). Therefore, the pressure gage at point C reads Po – This measurement, in conjunction with a measurement of the static pressure p at point A, yields the difference between total and static pressure, po — Pi, and it is this pressure difference that allows the calculation of Vj via Bernoulli’s equation. In particular, apply Bernoulli’s equation between point A, where the pressure and velocity are p and V, respectively, and point B, where the pressure and velocity are po and V = 0, respectively:

Solving Equation (3.33) for Vj, we have

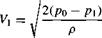[3.34]

Equation (3.34) allows the calculation of velocity simply from the measured difference between total and static pressure. The total pressure po is obtained from the Pitot tube, and the static pressure p is obtained from a suitably placed static pressure tap.

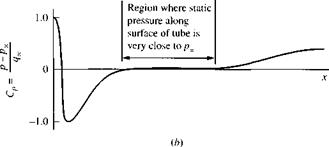
It is possible to combine the measurement of both total and static pressure in one instrument, a Pitot-static probe, as sketched in Figure 3.12. A Pitot-static probe measures po at the nose of the probe and p at a suitably placed static pressure tap on the probe surface downstream of the nose.

In Equation (3.33), the term Vj2 is called the dynamic pressure and is denoted by the symbol q. The grouping pV2 is called the dynamic pressure by definition

Figure 3.12 Pitot-static probe.

and is used in all flows, incompressible to hypersonic:

q = pV2

However, for incompressible flow, the dynamic pressure has special meaning; it is precisely the difference between total and static pressure. Repeating Equation (3.33), we obtain

	P +	pVi =	Po
	static	dynamic	total
	pressure	pressure	pressure
or	pi	+ q – po

or

qі = Po ~ Pi

[3.35]

It is important to keep in mind that Equation (3.35) comes from Bernoulli’s equation, and thus holds for incompressible flow only. For compressible flow, where Bernoulli’s equation is not valid, the pressure difference p0 — p is not equal to q. Moreover, Equation (3.34) is valid for incompressible flow only. The velocities of compressible flows, both subsonic and supersonic, can be measured by means of a Pitot tube, but the equations are different from Equation (3.34). (Velocity measurements in subsonic and supersonic compressible flows are discussed in Chapter 8.)

At this stage, it is important to repeat that Bernoulli’s equation holds for incom­pressible flow only, and therefore any result derived from Bernoulli’s equation also holds for incompressible flow only, such as Equations (3.26), (3.32), and (3.34). Ex­perience has shown that some students when first introduced to aerodynamics seem to adopt Bernoulli’s equation as the gospel and tend to use it for all applications, including many cases where it is not valid. Hopefully, the repetitive warnings given above will squelch such tendencies.

An airplane is flying at standard sea level. The measurement obtained from a Pitot tube mounted on the wing tip reads 2190 lb/ft2. What is the velocity of the airplane?

Solution

Standard sea level pressure is 2116 lb/ft2. From Equation (3.34), we have

2(po-Pi) = /2(2190 — 21167 p V 0.002377

In the wind-tunnel flow described in Example 3.4, a small Pitot tube is mounted in the flow just upstream of the model. Calculate the pressure measured by the Pitot tube for the same flow conditions as in Example 3.4.

Solution

From Equation (3.35),

Po — Poo “Ь Чоо — Poo “h 2 Poo

= 2116+ 4(0.002377)(328.4)2

= 2116+ 128.2 =

Note in this example that the dynamic pressure is ^Дх> = 128.2 lb/ft2. This is only 8 percent larger than the pressure difference (p — /+), calculated in Example 3.4, that is required to produce the test-section velocity in the wind tunnel. Why is (pi — po) so close to the test-section dynamic pressure? Answer: Because the velocity in the settling chamber Vi is so small that p is close to the total pressure of the flow. Indeed, from Equation (3.22),

v’ = J[Vl = (їг) (328’4) = 213 ft/s

Compared to the test-section velocity of 328.4 ft/s, V is seen to be small. In regions of a flow where the velocity is finite but small, the local static pressure is close to the total pressure. (Indeed, in the limiting case of a fluid with zero velocity, the local static pressure is the same as the total pressure; here, the concepts of static pressure and total pressure are redundant. For example, consider the air in the room around you. Assuming the air is motionless, and assuming standard sea level conditions, the pressure is 2116 lb/ft2, namely, 1 atm. Is this pressure a static pressure or a total pressure? Answer: It is both. By the definition of total pressure given in the present section, when the local flow velocity is itself zero, then the local static pressure and the local total pressure are exactly the same.)

Design Box The configuration of the Pitot-static probe shown in Figure 3.12 is a schematic only. The design of an actual Pitot-static probe is an example of careful engineering, intended to provide as accurate an instrument as possible. Let us examine some of the overall features of Pitot-static probe design. Above all, the probe should be a long, streamlined shape such that the surface pressure over a substantial portion of the probe is essentially equal to the free stream static pressure. Such a shape is given in Figure 3.13a. The head of the probe, the nose at which the total pressure is measured, is usually a smooth hemispherical shape in order to encourage smooth, streamlined flow downstream of the nose. The diameter of the tube is denoted by d. A number of static pressure taps are arrayed radially around the circumference of the tube at a station that should be from 8d to 16d downstream of the nose, and at least 16<з? ahead of the downstream support stem. The reason for

– 14 d	20 d
Stagnation point Total pressure measured here
(«) Figure 3.13 (a) Pitot-static tube, (b) Schematic of the pressure distribution along the outer surface of the tube.
this is shown in Figure 3.13b, which gives the axial distribution of the pressure coefficient along the surface of the tube. From the definition of pressure coefficient given in Section 1.5, and from Bernoulli’s equation in the form of Equation (3.35), the pressure coefficient at a stagnation point for incompressible flow is given by C, = = ^ = 1.0 с Цэc Hence, in Figure 3.13b the Cp distribution starts out at the value of 1.0 at the nose, and rapidly drops as the flow expands around the nose. The pressure decreases below px, yielding a minimum value of Cp ~ —1.25 just downstream of the nose. Further downstream the pressure tries to recover and approaches a value nearly equal to px at some distance (typically about 8d) from the nose. There follows a region where the static pressure along the surface of the tube is very close to px, illustrated by the region where Cp = 0 in Figure 3.13b. This is the region where the static pressure taps should be located, because the surface pressure measured at these taps will be essentially equal to the freestream static pressure px. Further downstream, as the flow approaches the support stem, the pressure starts to increase above px. This starts at a distance of about 16d ahead of the support stem. In Figure 3.13a, the static pressure taps are shown at a station 14d downstream of the nose and 20d ahead of the support stem. The design of the static pressure taps themselves is critical. The surface around the taps should be smooth to insure that the pressure sensed inside the tap is indeed the surface pressure along the tube. Examples of poor design as well as the proper design of the pressure taps are shown in Figure 3.14. In Figure 3.14a, the surface has a burr on the upstream side; the local flow will expand around this burr, causing the pressure sensed at point a inside the tap to be less than px. In 3.14 b, the surface has a burr on the downstream side; the local flow will be

slowed in this region, causing the pressure sensed at point b inside the tap to be greater than p^. The correct design is shown in Figure 3.14c; here, the opening of the tap is exactly flush with the surface, allowing the pressure sensed at point c inside the tap to be equal to p When a Pitot-static tube is used to measure the speed of an airplane, it should be located on the airplane in a position where it is essentially immersed in the freestream flow, away from any major influence of the local flow field around the airplane itself. An example of this can be seen in Figure 3.2, where a Pitot-static probe can be seen mounted near the right wing tip of the P-35, extending into the freestream ahead of the wing. A similar wing-mounted probe is shown in the planview (top view) of the North American F-86 in Figure 3.15. Today, many modem airplanes have a Pitot tube mounted at some location on the fuselage, and the measurement of poo is obtained independently from a properly placed static pressure tap somewhere else on the fuselage. Figure 3.16 illustrates a fuselage-mounted Pitot tube in the nose region of the Boeing Stratoliner, a 1940s vintage airliner. When only a Pitot measurement is required, the probe can be much shorter than a Pitot-static tube, as can be seen in Figure 3.16. In this type of arrangement, the location of the static pressure tap on the surface of the fuselage is critical; it must be located in a region where the surface pressure on the fuselage is equal to pa0. We have a pretty good idea where to locate the static pressure taps on a Pitot-static tube, as shown in Figure 3.13a. But the proper location on the fuselage of a given airplane must be found experimentally, and it is different for different airplanes. However, the basic idea is illustrated in Figure 3.17, which shows the measured pressure coefficient distribution over a streamlined body at zero angle of attack. There are two axial stations where Cp = 0 (i. e., where the surface pressure on the body equals p~,_). If this body were an airplane fuselage, the static pressure tap should be placed at one of these two locations. In practice, the forward location, near the nose, is usually chosen. Finally, we must be aware that none of these instruments, no matter where they are located, are perfectly accurate. In particular, misalignment of the probe with respect to the freestream direction causes an error which must be assessed for each particular case. Fortunately, the measurement of the total pressure by means of a Pitot tube is relatively insensitive to misalignment. Pitot tubes with hemispherical noses, such as shown in Figure 3.13a, are insensitive to the mean flow direction up to a few degrees. Pitot tubes with flat faces, such as illustrated in Figure 3.12, are least sensitive. For these tubes, the total pressure measurement varies only 1 percent for misalignment as large as 20°. For more details on this matter, see Reference 65.

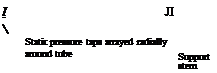Figure 3.15 Three-view of the North American F-86H. Note the wing-mounted Pitot-static tube.

Pitot tube

Figure 3.16 Nose-mounted Pitot tube on the Boeing Stratoliner. (Stratoliner detail courtesy of Paul Matt, Alan and Drina Abel, and Aviation Heritage, Inc., with permission.)

Experimentally measured pressure coefficient distribution over a streamlined body with a fineness ratio (length-to-diameter ratio) of 3. Zero angle of attack. Low-speed flow.

Figure 3.17