POINT SINGULARITY SOLUTIONS

The basic idea behind point singularity solutions is presented schematically in Fig. 11.1. If an exact solution in the form of a continuous singularity distribution (e. g., a vortex distribution y(x)) exists, then it can be divided into several finite segments (e. g., the segment between >x2). The local average strength of the element is then Г0 = у(дг) dx and it can be placed at a point x0 within the interval xx-x2. A discrete-element numerical solution can be obtained by specifying N such unknown element strengths and then estab-

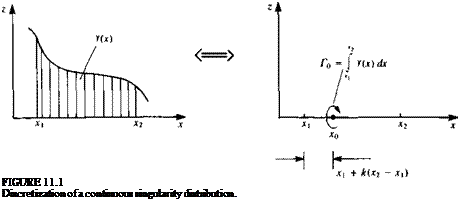
lishing N equations for their solution. This can be done by specifying the boundary conditions at N points along the boundary (and these points are called collocation points). Also, when constructing the solution, some of the considerations mentioned in Section 9.3 (e. g., in regard to the Kutta condition and the wake) must be addressed.

As a first example, this very simple approach is used for solving the lifting and thickness problems of thin airfoils, which were treated analytically in Chapter 5.