Potential Jump of Unsteady Vortex Sheet

The physical zero pressure jump requirement across a vortex sheet was combined with the steady Bernoulli equation in Section 5.4 to obtain the convection condition (5.15) for the potential jump. For the unsteady case this needs to be re-examined because of the additional term in the unsteady Bernoulli equation (7.19). We therefore consider an unsteady vortex sheet shown in Figure 7.3 which has separate potentials and velocities on its upper and lower sides. The vortex sheet can represent either a thin lifting surface or a wake.

Figure 7.3: Perturbation potential isolines and airfoil-frame velocities above and below an unsteady vortex sheet, on the airfoil and on the wake.

As in the steady case, a thin unsteady wake has the same physical requirement of a zero static pressure jump Ap = pi — pu across it. Taking the difference of the unsteady pressure expression (7.20) between a lower and upper point across the sheet, and setting the result to zero gives

Ap = 0 ->• I (V„-V„ – V/ • V/) + (фи – фі) = 0

5 (V„ + V) • (V„ – V/) + (фи – Фі) = о

Va -V (Ap) + (alp) = 0 (7.21)

where Vu, Vi are the upper and lower Vrei velocities, Va is the average sheet velocity

У а = l2 (V„ + V)

and V() is the surface gradient within the sheet. Note that (7.21) reduces to the earlier steady-flow potential jump result (5.15) if we set (a p) = 0.

3.1.1 Potential-jump convection

The unsteady wake zero pressure jump condition (7.21) can be rewritten as a substantial derivative.

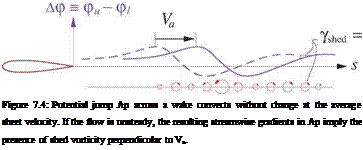
Equation (7.22) implies that the wake potential jump Ap(s, e,t) = pu—pi, set initially at the trailing edge by the Kutta condition, convects unchanged at the sheet velocity Va, as sketched in Figure 7.4.

3.1.2 Shed vorticity

From Figure 7.3 we see that the wake sheet has a tangential velocity jump Vu — Vi = V (Ap), which corresponds to a vortex sheet of the following strength.

дАф

ds

The trailing vorticity is the streamwise component of this 7 vector, and the shed vorticity is the transverse component. Choosing the s coordinate to be parallel to Va,

V0

|Va|

gives the following explicit definitions of the trailing and shed vorticity components.

Ytraii = s ■ 7 (7.25)

Yshed = (sX7) • n = s-V(Ap) = ^7 (7.26)

Comparing equation (7.26) with (7.21) together with the s definition shows that Yshed can be alternatively given by the time rate of Ap.

(лр) J = 0 , steady flow

|Va| =0 , unsteady flow

Shed vorticity is therefore present only in unsteady flows, and is a major complication in the formulation of unsteady potential flow calculation methods.