Prandtl Lifting Line Theory

15.8.2.1 Circulation Representation

A paper airplane wing is made of manila folder paper by cutting an ellipse of large aspect ratio (b, c0). Then the wing is given some small camber such that the relative camber is constant (d/c = const) along the span, and there is no twist, t (y) = 0. The circulation for an arbitrary wing is represented by a Fourier series

■ Г[y(ff)] = 2Ub X“=1 An sin n0
y(Q) = – j cos в, 0 < в < п

The chord distribution of the wing can be expressed as с[у(в)] = cxsine with the above change of variable.

Prandtl Integro-differential equation reads

where ai (y) = ww(y)/U is the induced angle of attack. Taking into account the wing characteristics, i. e. the constant relative camber, the absence of twist and the elliptic chord distribution, as seen in class, the above equation is satisfied identically with an elliptic loading since the corresponding downwash or induced incidence is constant as well. The relationship between the root circulation Г0, the incidence a, the constant induced incidence ai and the relative camber d/c reduces to

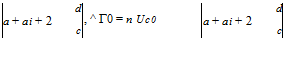
Г0 sine

15.8.2.2 Ideal Angle of Attack

From the previous result, one can calculate the lift coefficient, starting with

d 2Г0 d

Г0 = 2nUc0 , ^ Cl = – = 4п

c Uc0 c

The geometric incidence, aideai that will make the effective incidence zero, i. e. aeff = aideai + ai = 0 is such that

See Fig. 15.34.