Pressure calculation

Chapter 1 gave the derivation if the unsteady Bernoulli equation (1.105) for incompressible flow:

Here we have V2 = |Vp|2, and we will also absorb the hydrostatic term gz into р/р, as described in Section 1.9.3. The integration constant C can be evaluated at any point where the pressure and velocity are known, such as at infinity where p = pL, and where the fluid is at rest so that all p derivatives vanish.

It’s essential to note that (7.15) as written applies only in an inertial frame of reference, since it was ul­timately derived from the momentum equation (1.86) for which we set f to be gravity, omitting any non­inertial forces. This is why we chose U2 = |Vp|2, and not U2 = |Vrei|2- Furthermore, the time derivative dp/dt must be performed at a spatial point which is inertial, meaning that this point is either stationary (VL = 0) or at most translating with uniform speed (VL = 0) relative to Earth. Specifically, the time deriva­tive must not be performed at a point fixed on an accelerating or rotating body.

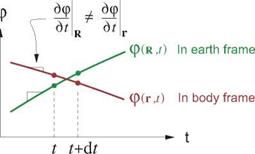
A practical complication here is that because the solution to the potential-flow problem as formulated above is given in the body coordinates in the form p(r, t), its explicit time derivative is at fixed r which is not an inertial point. However, we require a time derivative at fixed R which is inertial. The distinction between the time derivatives in the two frames is shown in Figure 7.2.

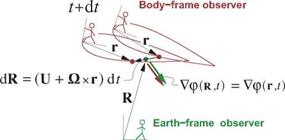Figure 7.2: Potential-field time variation at a point R fixed in the Earth frame, and another point r fixed in the body frame. At the moment when the points coincide, the p and Vp values in the two frames are equal, but the time derivatives dp/dt are not.

To perform the frame conversion, we first note from Figure 7.1 that positions in the two frames are related by the correspondence function R(r, t) which obeys

which can then be used to relate time derivatives in the two frames. Considering the potential to be in the form p(R(r, t),t), we obtain its time rate in the body frame via the chain rule,

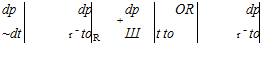
(7.16)

where dp/dR is just a more intuitive way to write the spatial gradient Vp in this context. Relation (7.16) then gives the potential’s time-rate in the Earth frame entirely in terms of quantities in the body frame.

Pir,*) = Poo ~ p |Vtp|2 + pVp • (U + Oxr) – pp

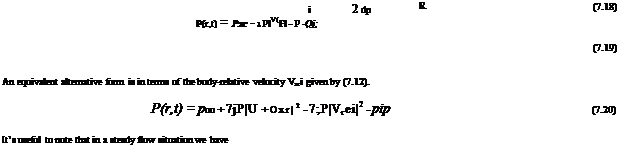The pressure can now be expressed using the unsteady Bernoulli equation (7.15) applied in the frame of the Earth-based observer in Figure 7.2:

U = —V О = 0

p = 0

in which case (7.20) reduces to the familiar steady Bernoulli equation.

P(r, t) = Poo + ЗРК2 – 5PlVrel|2