Pressure Coefficient

Pressure, by itself, is a dimensional quantity (e. g., pounds per square foot, newtons per square meter). However, in Sections 1.7 and 1.8, we established the usefulness of certain dimensionless parameters such as M, Re, Cl – It makes sense, therefore, that a dimensionless pressure would also find use in aerodynamics. Such a quantity is the pressure coefficient Cp, first introduced in Section 1.5 and defined as

where qoo = pooVl-t

The definition given in Equation (3.36) is just that—a definition. It is used throughout aerodynamics, from incompressible to hypersonic flow. In the aerodynamic literature, it is very common to find pressures given in terms of Cp rather than the pressure itself. Indeed, the pressure coefficient is another similarity parameter that can be added to the list started in Sections 1.7 and 1.8.

For incompressible flow, Cp can be expressed in terms of velocity only. Consider the flow over an aerodynamic body immersed in a freestream with pressure Poo and velocity Toe. Pick an arbitrary point in the flow where the pressure and velocity are p and V, respectively. From Bernoulli’s equation,

Poo + ‘oPV^ = P + {pV2

or p – Poo = У (Vi – V2) [3.37]

Substituting Equation (3.37) into (3.36), we have

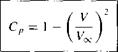„ P – Poo p{V2oo – V2) p – „ ~ і „1/2

Equation (3.38) is a useful expression for the pressure coefficient; however, note that the form of Equation (3.38) holds for incompressible flow only.

Note from Equation (3.38) that the pressure coefficient at a stagnation point (where V = 0) in an incompressible flow is always equal to 1.0. This is the highest allowable value of Cp anywhere in the flow field. (For compressible flows, Cp at a stagnation point is greater than 1.0, as shown in Chapter 14.) Also, keep in mind that in regions of the flow where V > Vx or p < Poo, Cp will be a negative value.

Another interesting property of the pressure coefficient can be seen by rearranging the definition given by Equation (3.36), as follows:

P = Рос + ЧосСр

Clearly, the value of Cp tells us how much p differs from p^ in multiples of the dynamic pressure. That is, if Cp = 1 (the value at a stagnation point in an incom­pressible flow), then p = рос + q<oc, or the local pressure is “one times” the dynamic pressure above freestream static pressure. If Cp — —3, then p = p0Q — 3qoo, or the local pressure is three times the dynamic pressure below freestream static pressure.

Example 3. 7 I Consider an airfoil in a flow with a freestream velocity of 150 ft/s. The velocity at a given point
on the airfoil is 225 ft/s. Calculate the pressure coefficient at this point.

225 V[7] [8] [9] І50 /

Solution

speed of sound at standard sea level is 1117 ft/s; hence, the freestream Mach number is 300/1117 = 0.269. A flow where the local Mach number is less than 0.3 can be assumed to be essentially incompressible. Hence, the freestream Mach number satisfies this criterion. On the other hand, the flow rapidly expands over the top surface of the airfoil and accelerates to a velocity of 753 ft/s at the point of minimum pressure (the point of peak negative Cp). In the expansion, the speed of sound decreases. (We will find out why in Part 3.) Hence, at the point of minimum pressure, the local Mach number is greater than = 0.674. That is, the flow has expanded to such a high local Mach number that it is no longer incompressible. Therefore, the answer given in part (b) of Example 3.8 is not correct. (We will learn how to calculate the correct value in Part 3.) There is an interesting point to be made here. Just because a model is being tested in a low-speed, subsonic wind tunnel, it does not mean that the assumption of incompressible flow will hold for all aspects of the flow field. As we see here, in some regions of the flow field around a body, the flow can achieve such high local Mach numbers that it must be considered as compressible.