Pressure Drag

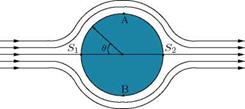
The pressure drag arises due to the separation of boundary layer, caused by adverse pressure gradient. The phenomenon of separation, and how it causes the pressure drag, can be explained by considering flow around a body, such as a circular cylinder. If the flow is assumed to be potential, there is no viscosity and hence no boundary layer. The flow past the cylinder would be as shown in Figure 2.22, without any separation.

Potential flow around a cylinder will be symmetrical about both the horizontal and vertical planes, passing through the center of the cylinder. The pressure distribution over the front and back surfaces would be identical, and the net force along the freestream direction would be zero. That is, there would

not be any drag acting on the cylinder. But in real flow, because of viscosity, a boundary layer is formed over the surface of the cylinder. The flow experiences a favorable pressure gradient from the forward stagnation point to the topmost point A on the cylinder at в = 90°, shown in Figure 2.22.

Therefore, the flow accelerates from point to A (that is, from в = 0° to 90°). However, beyond

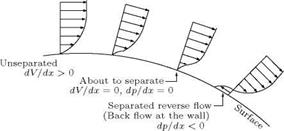
в = 90° the flow is subjected to an adverse pressure gradient and hence decelerates. Note that beyond the topmost point A the fluid elements find a larger space to relax. Therefore, in accordance with mass conservation (for subsonic flow) [2], as the flow area increases the flow speed decreases and the pressure increases. Under this condition there is a net pressure force acting against the fluid flow. This process establishes an adverse pressure gradient, leading to flow separation, as illustrated in Figure 2.23. In a boundary layer, the velocity near the surface is small, and hence the force due to its momentum is unable to counteract the pressure force. Flow within the boundary layer gets retarded and the velocity near the wall region reduces to zero at some point downstream of A and then the flow is pushed back in the opposite direction, as illustrated in Figure 2.23. This phenomenon is called flow separation.

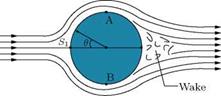
The location where the flow leaves the body surface is termed separation point. For flow past a cylinder, there are two separation points on either side of the horizontal axis through the center of the cylinder. The separated flow is chaotic and vortex dominated. The separated flow behind an object is also referred to as wake. Depending on the Reynolds number level, the wake may be laminar or turbulent. An important characteristics of the separated flow is that it is always unsymmetrical, even for laminar

separation. This is because of the vortices prevailing in the separated zone. As we know, for every vortex there is a specific frequency and amplitude. Therefore, when the vortices formed at the upper and lower separation points of the cylinder are of the same size and leave the cylinder at the same time, the wake must be symmetric. But this kind of formation of vortices of identical size and leaving the upper and lower separation points at the same time is possible only when the geometry of the cylinder is perfectly symmetrical and the freestream flow is absolutely unperturbed and symmetrical about the horizontal plane bisecting the cylinder. But in practice it is not possible to meet these stringent requirements of flow and geometrical symmetry to establish symmetrical separation. Owing to this practical constraints all separated flows are unsymmetrical. Indeed, the formation of the vortices at the upper and lower separation points itself is unsymmetrical. When one of them, say the upper one, grows faster, the other one is unable to grow at the same rate. Therefore, only after the faster growing vortex reaches a limiting size possible, for the geometry and Reynolds number combination, and leaves the surface, the growth of the vortex at the opposite side picks up. This retards the growth of the new vortex formed at the location where the vortex left the surface. Thus, alternative shedding of vortices from the upper and lower separation points is established. The alternative shedding of vortices makes the wake chaotic.

Across the separated region, the total pressure is nearly a constant and lower than what it would have been if the flow did not separate. The pressure do not recover completely as in the case of potential flow. Thus, on account of the incomplete recovery of pressure due to separation, a net drag force opposing the body motion is generated. We can easily see that the pressure drag will be small if the separation had taken place later, that is, the area over which the pressure unrecovered is small. To minimize pressure drag, the separation point should be as far as possible from the leading edge or forward stagnation point. This is true for any shape. Streamlined bodies are designed on this basis and the adverse pressure gradient is kept as small as possible, by keeping the curvature very small. At this stage, it is important to realize that the separated region behind an object is vortex dominated and these vortices cause considerable pressure loss. Thus the total pressure _P0,rear behind the object is significantly lower than the total pressure _P0,face at the face of the object. This difference (p0,rear — _P0,face), termed pressure loss, is a direct measure of the drag. This drag caused by the pressure loss is called the pressure drag. This is also referred to as form drag, because the form or shape of the moving object dictates the separation and the expanse of the separated zone. The separation zone behind an object is also referred to as wake. That is, wake is the separated region behind an object (usually a bluff body) where the pressure loss is severe. It is essential to note that what is meant by pressure loss is total pressure loss, and there is nothing like static pressure loss.

The separation of boundary layer depends not only on the strength of the adverse pressure gradient but also on the nature of the boundary layer, namely, laminar or turbulent. A laminar flow has tendency to separate earlier than a turbulent flow. This is because the laminar velocity profiles in a boundary layer has lesser momentum near the wall. This is conspicuous in the case of flow over a circular cylinder. Laminar boundary layer separates nearly at в = 90° whereas, for a highly turbulent boundary layer the separation is delayed and the attached flow continues up to as far as в = 150° on the cylinder. The reduction of pressure drag when the boundary layer changes from laminar to turbulent is of the order of 5 times for bluff bodies. The flow behind a separated region is called the wake. For low drag, the wake width should be small.

Although separation is shown to take place at well defined locations on the body, in the illustration in Figure 2.23, it actually takes places over a zone on the surface which can not be identified easily. Therefore, theoretical estimation of separation especially for a turbulent boundary layer is difficult and hence the pressure drag cannot be easily calculated. Some approximate methods exist but they can serve only as guidelines for the estimation of pressure drag.

At this stage, we may wonder about the level of static pressure in the separated flow region or the wake of a body. The total pressure in the wake is found to be lower than that in the freestream, because of the pressure loss caused by the vortices in the wake. But the static pressure in the wake is almost equal to the freestream level. But it is essential to realize that just after separation, the flow is chaotic and the streaklines do not exhibit any defined pattern. Therefore, the static pressure does not show any specific mean value in the near-wake region and keeps fluctuating. However, beyond some distance behind the
object, the wake stabilizes to an extent to assume almost constant static pressure across its width. This distance is about 6 times the diameter for a circular cylinder. Thus, beyond 6 diameter distance the static pressure in the wake is equal to the freestream value.

Note: It may be useful to recall what is meant by pressure loss is the total pressure loss and there is nothing like static pressure loss.