Relationship Between the Stream Function and Velocity Potential

In Section 2.15, we demonstrated that for an irrotational flow Y = Уф. At this stage, take a moment and review some of the nomenclature introduced in Section 2.2.5 for the gradient of a scalar field. We see that a line of constant ф is an isoline of ф; since ф is the velocity potential, we give this isoline a specific name, equipotential line. In addition, a line drawn in space such that Уф is tangent at every point is defined as a gradient line; however, since Уф = V, this gradient line is a streamline. In turn, from Section 2.14, a streamline is a line of constant Ф (for a two-dimensional flow). Because gradient lines and isolines are perpendicular (see Section 2.2.5, Gradient of a Scalar Field), then equipotential lines (ф = constant) and streamlines (ф = constant) are mutually perpendicular.

To illustrate this result more clearly, consider a two-dimensional, irrotational, incompressible flow in cartesian coordinates. For a streamline, ф(х, у) = constant. Hence, the differential of ф along the streamline is zero; i. e.,

[2.159]

From Equation (2.150a and b), Equation (2.159) can be written as

йф = —v dx + и dy = 0

2 ф (or тД) can be defined for axisymmetric flows, such as the flow over a cone at zero degrees angle of attack. However, for such flows, only two spatial coordinates are needed to describe the flow field (see Chapter 6).

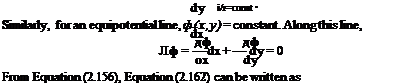Solve Equation (2.160) for dy/dx, which is the slope of the ф = constant line, i. e., the slope of the streamline:

dф = и dx + v dy = 0

Solving Equation (2.163) for dy /dx, which is the slope of the ф — constant line, i. e., the slope of the equipotential line, we obtain

Equation (2.165) shows that the slope of а ф = constant line is the negative reciprocal of the slope of а ф = constant line, i. e., streamlines and equipotential lines are mutually perpendicular.