Review of Vector Relations

Aerodynamics is full of quantities that have both magnitude and direction, such as force and velocity. These are vector quantities, and as such, the mathematics of aerodynamics is most conveniently expressed in vector notation. The purpose of this section is to set forth the basic relations we need from vector algebra and vector calculus. If you are familiar with vector analysis, this section will serve as a concise review. If you are not conversant with vector analysis, this section will help you establish some vector notation, and will serve as a skeleton from which you can fill in more information from the many existing texts on vector analysis (see, e. g., References 4 to 6).

2.2.1 Some Vector Algebra

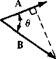
Consider a vector quantity A; both its magnitude and direction are given by the arrow labeled A in Figure 2.2. The absolute magnitude of A is |A|, and is a scalar quantity. The unit vector n, defined by n = A/|A|, has a magnitude of unity and a direction equal to that of A. Let В represent another vector. The vector addition of A and В yields a third vector C,

A + B = C

which is formed by connecting the tail of A with the head of B, as shown in Figure 2.2. Now consider —B, which is equal in magnitude to B, but opposite in direction. The vector subtraction of В and A yields vector D,

A – В = D

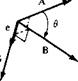
Figure 2.2 Vector diagrams.

which is formed by connecting the tail of A with the head of —B, as shown in Figure 2.2.

There are two forms of vector multiplication. Consider two vectors A and В at an angle в to each other, as shown in Figure 2.2. The scalar product (dot product) of the two vectors A and В is defined as

A • В = IAI |B I cos0 [2.3]

= magnitude of A x magnitude of the component of В along the direction of A

Note that the scalar product of two vectors is a scalar. In contrast, the vector product (cross product) of the two vectors A and В is defined as

A x В = (|A||B| sin0)e = G [2.4]

where G is perpendicular to the plane of A and В and in a direction which obeys the “right-hand rule.” (Rotate A into B, as shown in Figure 2.2. Now curl the fingers of your right hand in the direction of the rotation. Your right thumb will be pointing in the direction of G.) In Equation (2.4), e is a unit vector in the direction of G, as also shown in Figure 2.2. Note that the vector product of two vectors is a vector.