Road Map for This Chapter

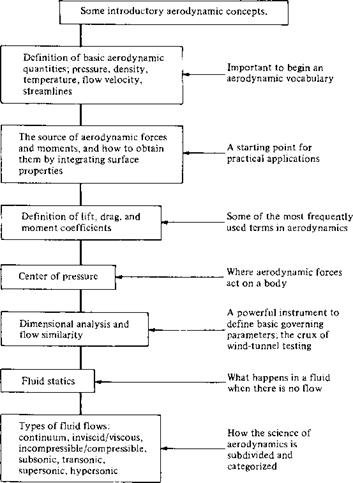
When learning a new subject, it is important for you to know where you are, where you are going, and how you can get there. Therefore, at the beginning of each chapter in this book, a road map will be given to help guide you through the material of that chapter and to help you obtain a perspective as to how the material fits within the general framework of aerodynamics. For example, a road map for Chapter 1 is given in Figure 1.6. You will want to frequently refer back to these road maps as you progress through the individual chapters. When you reach the end of each chapter, look back over the road map to see where you started, where you are now, and what you learned in between.

1.3 Some Fundamental Aerodynamic Variables

A prerequisite to understanding physical science and engineering is simply learn­ing the vocabulary used to describe concepts and phenomena. Aerodynamics is no exception. Throughout this book, and throughout your working career, you will be adding to your technical vocabulary list. Let us start by defining four of the most frequently used words in aerodynamics: “pressure,” “density,” “temperature,” and “flow velocity.”1

Consider a surface immersed in a fluid. The surface can be a real, solid surface such as the wall of a duct or the surface of a body; it can also be a free surface which we simply imagine drawn somewhere in the middle of a fluid. Also, keep in mind that

Figure 1 .6 Road map for Chapter 1.

the molecules of the fluid are constantly in motion. Pressure is the normal force per unit area exerted on a surface due to the time rate of change of momentum of the gas molecules impacting on (or crossing) that surface. It is important to note that even though pressure is defined as force “per unit area,” you do not need a surface that is exactly 1 ft2 or 1 m2 to talk about pressure. In fact, pressure is usually defined at a point in the fluid or a point on a solid surface and can vary from one point to another. To see this more clearly, consider a point В in a volume of fluid. Let

dA — elemental area at В

dF = force on one side of dA due to pressure

Then, the pressure at point В in the fluid is defined as

dF ~dA
p = lim	dA
0

The pressure p is the limiting form of the force per unit area, where the area of interest has shrunk to nearly zero at the point B.[1] Clearly, you can see that pressure is a point property and can have a different value from one point to another in the fluid.

Another important aerodynamic variable is density, defined as the mass per unit volume. Analogous to our discussion on pressure, the definition of density does not require an actual volume of 1 ft[2] or 1 m3. Rather, it is a point property that can vary from point to point in the fluid. Again, consider a point В in the fluid. Let

dv = elemental volume around В dm — mass of fluid inside dv Then, the density at point В is

dm

p = lim—— dv —»■ 0

dv

Therefore, the density p is the limiting form of the mass per unit volume, where the volume of interest has shrunk to nearly zero around point B. (Note that dv cannot achieve the value of zero for the reason discussed in the footnote concerning dA in the definition of pressure.)

Temperature takes on an important role in high-speed aerodynamics (introduced in Chapter 7). The temperature Г of a gas is directly proportional to the average kinetic energy of the molecules of the fluid. In fact, if KE is the mean molecular kinetic energy, then temperature is given by ICE = |kT, where к is the Boltzmann constant. Hence, we can qualitatively visualize a high-temperature gas as one in which the molecules and atoms are randomly rattling about at high speeds, whereas in a low-temperature gas, the random motion of the molecules is relatively slow. Temperature is also a point property, which can vary from point to point in the gas.

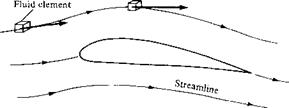
The principal focus of aerodynamics is fluids in motion. Hence, flow velocity is an extremely important consideration. The concept of the velocity of a fluid is slightly more subtle than that of a solid body in motion. Consider a solid object in translational motion, say, moving at 30 m/s. Then all parts of the solid are simul­taneously translating at the same 30 m/s velocity. In contrast, a fluid is a “squishy” substance, and for a fluid in motion, one part of the fluid may be traveling at a different velocity from another part. Hence, we have to adopt a certain perspective, as follows. Consider the flow of air over an airfoil, as shown in Figure 1.7. Lock your eyes on a specific, infinitesimally small element of mass in the gas, called a fluid element, and watch this element move with time. Both the speed and direction of this fluid element can vary as it moves from point to point in the gas. Now fix your eyes on a specific fixed point in space, say, point В in Figure 1.7. Flow velocity can now be defined as follows: The velocity of a flowing gas at any fixed point В in space is the velocity of an infinitesimally small fluid element as it sweeps through B. The flow velocity V has both magnitude and direction; hence, it is a vector quantity. This is in contrast to p, p, and T, which are scalar variables. The scalar magnitude of V is frequently

В Figure 1.7 Illustration of flow velocity and streamlines.

used and is denoted by V. Again, we emphasize that velocity is a point property and can vary from point to point in the flow.

Referring again to Figure 1.7, a moving fluid element traces out a fixed path in space. As long as the flow is steady, i. e., as long as it does not fluctuate with time, this path is called a streamline of the flow. Drawing the streamlines of the flow field is an important way of visualizing the motion of the gas; we will frequently be sketching the streamlines of the flow about various objects. A more rigorous discussion of streamlines is given in Chapter 2.