Solutions for Subsonic and Supersonic Flows
The outer flow is easily built up from a continuous distribution of sources along the ж-axis. The solution for a source in a subsonic flow is given by (5-37). Thus, for a distribution of strength f(x) per unit axial distance,
![]() J_ f f(xi) dxі
J_ f f(xi) dxі
4-7Г v/(x — Жі)2 + /32r2
The source strength must be determined such that the boundary condition (6-22) is satisfied. It follows directly from (6-22) that the volumetric outflow per unit length should be equal to the streamwise rate of change of cross-sectional area (multiplied by Ux). Hence we have
![]() / = S'(x).
/ = S'(x).
The result thus becomes
_ 1 £ <S'(xi) dx і
4:ir Jо л/(ж — xi)2 + /32r2
We need to expand the solution for small r in order to determine an inner solution of the form (6-24). This can be done in a number of ways, for example by Fourier transform techniques (Adams and Sears, 1953) or integration by parts. Here we shall select a method used by Oswatitsch
and Keune (1955) for its physical perspicuity. It is seen that the kernel in the integral (6-27) for small r is approximately
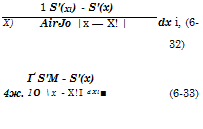 |
|
In the second term of (6-29) we may use the approximation (6-28) because the numerator tends to zero for xx —> x (the error actually turns out to be of order r2 In r). Thus, collecting all the terms in (6-29), we find that for small r
The last term gives the effect due to variation of source strength at body stations fairly far away from station x. This form of the integral is particularly convenient when the cross-sectional area distribution is given as a polynomial, since then the integrand will become a polynomial in xx. We may obtain an alternate form by performing an integration by parts in (6-33). This gives
cx
g(x) = ^~lnf — 4~ Jo s"(xi)ln (x — xi) dxx
+ Il-f S"(x0 ln (Xi — x) dxx, (6-34)
where we have assumed that S'(0) = S'(l) = 0, that is, the body has a pointed nose and ends in a point or in a cylindrical portion.
The solution for supersonic flow can be found in the same manner. Using (5-38) we obtain
rx—Br
1 S'(xi) dxx /n nr4
<p = — 7T~ – — – -—:———- _ ’ (6-35)
6ТГ J a /(x — Xl)2 — B2r2
where
В = VM2 – 1.
The upper integration limit follows because each source can only be felt inside its downstream Mach cone; hence the rearmost source that can influence the flow in the point x, r is located at xx = x — Br. Rewriting of (6-35) in a similar manner as (6-30) gives
(6-36)
For the first term we obtain
![]() dx 1
dx 1
уДх — xx)2 — B2r2
In the second integral we may replace the square root by x — xx as before. In addition, the upper integration limit may be replaced by x for
That the correct factor 1/27Г (cf. 6-24) was obtained for the first term confirms the constant for the supersonic source solution (5-38) selected by intuitive reasoning. For the supersonic case we thus have
As with subsonic flow, an alternate form can be obtained by integrating the last term by parts. This yields
where we have assumed that <8′(0) = 0. This form will be used later for the calculation of drag.
It is interesting to note how g(x) changes from subsonic to supersonic flow, as seen by comparing (6-34) with (6-40). First, /3 is replaced by B. Secondly, the integral
which represents the upstream influence in subsonic flow, changes to
— Jo s"(xi) ln (x — xi) dxb
that is, becomes equal to half the total downstream influence. To understand this behavior, consider the disturbance caused by a source in one cross section x as it is felt on the body at other cross sections. The disturbance will spread along two wave fronts, one wave moving downstream with a velocity of (approximately) ax + Ux and the other either upstream or downstream with a velocity of aw — Ux, depending on whether the flow is subsonic or supersonic. The effect of fast-moving waves is given by the first integral in (6-34), whereas that of slow-moving waves is given by the second integral. In the supersonic case, the fast and slow waves each contribute half of the integral in (6-40). Because of the small crosswise dimensions of the body, the curvature of the waves may be neglected in the present approximation. Hence their fronts may be treated as plane, the total effect being given by a function of x only.
|
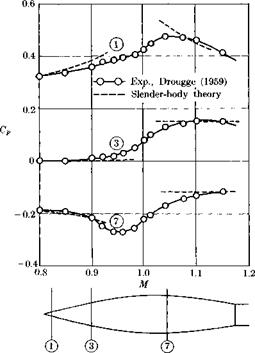
Fig. 6-і. Pressures on the forward portion on a body of revolution. [Adapted from Drougge (1959). Courtesy of Aeronautical Research Institute of Sweden.] |
A comparison of calculated and measured pressure distributions given by Drougge (1959) is shown in Fig. 6-1. The excellent agreement despite the fairly large thickness ratio (r = £) demonstrates the higher accuracy of slender-body theory than thin-airfoil theory. In the former theory the error term is of order e4 (or, rather, e4 In e), whereas in the latter it is of order e2. In assessing the accuracy of slender-body theory for practical cases, however, one must remember that the body considered in Fig. 6-1 is very smooth, with small second derivative of the cross-sectional area distribution, and should therefore be ideally suited for the theory.
The weak Mach number dependence of In |1 — Л/21 as compared to |1 — A/2|~1/2 in the thin-airfoil case, with the associated weaker singularity at M = 1, is significant. It indicates that the linearized slender-body theory generally holds closer to M = 1 than does the thin-airfoil theory for the same thickness ratio, i. e., the true transonic region should be much
smaller. For the body in Fig. 6-1, the linearized theory gives accurate pressure distributions for M < 0.90 and M > 1.10. In the transonic region the slow-moving waves will have time to interact and accumulate on the body, thus creating nonlinear effects that cannot be treated with the present linearized theory. The transonic case will be further discussed in Chapter 12.
Implicit in the derivation of the theory was the assumption that S’ is continuous everywhere, as is also evident from the results which show that <p becomes logarithmically singular at discontinuities of S’ and the pressure thus singular as the inverse of the distance. However, the slender-body theory may be considered as the correct “outer” solution away from the discontinuity with a separate “inner” solution required in its immediate neighborhood. Such a theory has in effect been developed by Lighthill (1948).