Some Aspects of Supersonic Flow: Shock Waves
Return to the different regimes of flow sketched in Figure 1.37. Note that subsonic compressible flow is qualitatively (but not quantitatively) the same as incompressible flow; Figure 1.37a shows a subsonic flow with a smoothly varying streamline pattern, where the flow far ahead of the body is forewarned about the presence of the body and begins to adjust accordingly. In contrast, supersonic flow is quite different, as sketched in Figure 1.37<i and e. Here, the flow is dominated by shock waves, and the flow upstream of the body does not know about the presence of the body until it encounters the leading-edge shock wave. In fact, any flow with a supersonic region, such as those sketched in Figure 1.37ft to e, is subject to shock waves. Thus, an essential ingredient of a study of supersonic flow is the calculation of the shape and strength of shock waves. This is the main thrust of Chapters 8 and 9.
A shock wave is an extremely thin region, typically on the order of 1СГ5 cm, across which the flow properties can change drastically. The shock wave is usually at an oblique angle to the flow, such as sketched in Figure 7.5a; however, there are many cases where we are interested in a shock wave normal to the flow, as sketched in Figure 7.5b. Normal shock waves are discussed at length in Chapter 8, whereas oblique shocks are considered in Chapter 9. In both cases, the shock wave is an almost explosive compression process, where the pressure increases almost discontinuously across the wave. Examine Figure 7.5 closely. In region 1 ahead of the shock, the Mach number, flow velocity, pressure, density, temperature, entropy, total pressure, and total enthalpy are denoted by p, p,T, s, ро. ь and /год, respectively.
The analogous quantities in region 2 behind the shock are М2, V2, pi, Pi> Ti, si, po,2> and /го,2, respectively. The qualitative change across the wave are noted in Figure 7.5. The pressure, density, temperature, and entropy increase across the shock, whereas the total pressure, Mach number, and velocity decrease. Physically, the flow across a shock wave is adiabatic (we are not heating the gas with a laser beam or cooling it in a refrigerator, for example). Therefore, recalling the discussion in Section 7.5, the total enthalpy is constant across the wave. In both the oblique shock and normal shock cases, the flow ahead of the shock wave must be supersonic (i. e., Mx > 1). Behind the oblique shock, the flow usually remains supersonic (i. e., М2 > 1), but at a reduced Mach number (i. e., М2 < M). However, as discussed in Chapter 9, there are special cases where the oblique shock is strong enough to decelerate the downstream flow to a subsonic Mach number; hence, M2 < 1 can occur behind an oblique shock. For the
![]()
 |
|
|
|
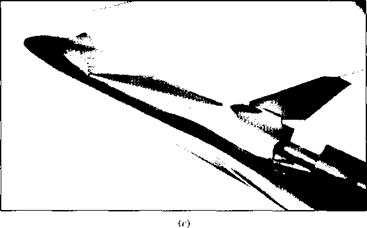
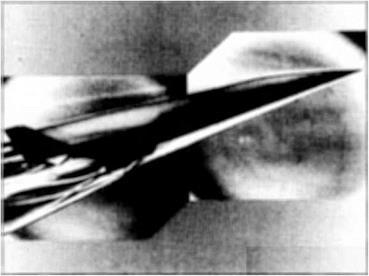
(d) Figure 7.6 (continued) (c) Space Shuttle Orbiter model at Mach 6. This photo also shows regions of high aerodynamic heating on the model surface by means of the visible phase-change paint pattern, (c/) A conceptual hypersonic aircraft at Mach 6. (Courtesy of the NASA Langley Research Center.) |
In summary, compressible flows introduce some very exciting physical phenomena into our aerodynamic studies. Moreover, as the flow changes from subsonic to supersonic, the complete nature of the flow changes, not the least of which is the occurrence of shock waves. The purpose of the next seven chapters is to describe and analyze these flows.