Special Forms of the Energy Equation
In this section, we elaborate upon the energy equation for adiabatic flow, as originally given by Equation (7.44). In Section 7.5, we obtained for a steady, adiabatic, inviscid flow the result that
where V and VA are velocities at any two points along a three-dimensional streamline. For the sake of consistency in our current discussion of one-dimensional flow, let us use и і and м2 in Equation (8.28):
2 2
MT ui, „
hi + – j – = h2 + у [8.39]
However, keep in mind that all the subsequent results in this section hold in general
along a streamline and are by no means limited to just one-dimensional flows.
Specializing Equation (8.29) to a calorically perfect gas, where h = cpT, we
have
From Equation (7.9), Equation (8.30) becomes
![]() yRTi _ yRT2 и| y-l+2~y-l+2
yRTi _ yRT2 и| y-l+2~y-l+2
Since a = л/уТТГ, Equation (8.31) can be written as
If we consider point 2 in Equation (8.32) to be a stagnation point, where the stagnation speed of sound is denoted by ao, then, with u2 = 0, Equation (8.32) yields (dropping the subscript 1)
In Equation (8.33), a and и are the speed of sound and flow velocity, respectively, at any given point in the flow, and ao is the stagnation (or total) speed of sound associated with that same point. Equivalently, if we have any two points along a streamline, Equation (8.33) states that
Recalling the definition of a* given at the end of Section 7.5, let point 2 in Equation (8.32) represent sonic flow, where и = a*. Then
In Equation (8.35), a and и are the speed of sound and flow velocity, respectively, at any given point in the flow, and a* is a characteristic value associated with that same point. Equivalently, if we have any two points along a streamline, Equation (8.35) states that
Comparing the right-hand sides of Equations (8.34) and (8.36), the two properties a0 and a* associated with the flow are related by
V + 1 *2 flQ r ,
——— – a*2 = —5— = const Ї8.37І
2(y – 1) У – 1
Clearly, these defined quantities, a0 and a*, are both constants along a given streamline in a steady, adiabatic, inviscid flow. If all the streamlines emanate from the same uniform freestream conditions, then a(l and a* are constants throughout the entire flow field.
Recall the definition of total temperature To, as discussed in Section 7.5. In Equation (8.30), let u2 = 0; hence T2 = 70. Dropping the subscript 1, we have
Equation (8.38) provides a formula from which the defined total temperature TQ can be calculated from the given actual conditions of T and и at any given point in a general flow field. Equivalently, if we have any two points along a streamline in a steady, adiabatic, inviscid flow, Equation (8.38) states that
2 2
CPT + Y = cpT2 + Y = CpTo = const [8.39]
If all the streamlines emanate from the same uniform freestream, then Equation (8.39) holds throughout the entire flow, not just along a streamline.
For a calorically perfect gas, the ratio of total temperature to static temperature То/T is a function of Mach number only, as follows. From Equations (8.38) and
(7.9) , we have
To і і и2 1 i и2 1 | и2
7 = 1 + 2c~^T = 1 + lyRT/iy – О = 1 + 2a2/(у – 1)
![]()
![]()
![]()
= 1 +
Equation (8.40) is very important; it states that only M (and, of course, the value of y) dictates the ratio of total temperature to static temperature.
Recall the definition of total pressure po and total density p0, as discussed in Section 7.5. These definitions involve an isentropic compression of the flow to zero velocity. From Equation (7.32), we have
![]()
|
|
||
|
|
||
|
|||
|
|||
Combining Equations (8.40) and (8.41), we obtain
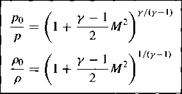 [8.42]
[8.42]
[8.43]
Similar to the case of Tq/T, we see from Equations (8.42) and (8.43) that the total – to-static ratios po/p and po/p are determined by M and у only. Hence, for a given gas (i. e., given y), the ratios T0/T, po/p, and po/p depend only on Mach number.
Equations (8.40), (8.42), and (8.43) are very important; they should be branded on your mind. They provide formulas from which the defined quantities 7b, po, and Po can be calculated from the actual conditions of M, T, p, and p at a given point in a general flow field (assuming a calorically perfect gas). They are so important that values of T0/T, p0/p, and po/p obtained from Equations (8.40), (8.42), and (8.43), respectively, are tabulated as functions of M in Appendix A for у = 1.4 (which corresponds to air at standard conditions).
Consider a point in a general flow where the velocity is exactly sonic (i. e., where M = 1). Denote the static temperature, pressure, and density at this sonic condition as T*, p*, and p*, respectively. Inserting M = 1 into Equations (8.40), (8.42), and
(8.43) , we obtain
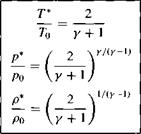 [8.44]
[8.44]
[8.45]
[8.48]
For у = 1.4, these ratios are
|
у * — = 0.833 |
p* — = 0.528 |
P* — = 0.634 |
|
To |
Po |
Po |
which are useful numbers to keep in mind for subsequent discussions.
We have one final item of business in this section. In Chapter 1, we defined the Mach number as M = V/a (or, following the one-dimensional notation in this chapter, M = и/a). In turn, this allowed us to define several regimes of flow, among them being
M < 1 (subsonic flow)
M = 1 (sonic flow)
M > 1 (supersonic flow)
In the definition of M, a is the local speed of sound, a = л/yRT. In the theory of supersonic flow, it is sometimes convenient to introduce a “characteristic” Mach number M* defined as
![]() и
и
a* where a* is the value of the speed of sound at sonic conditions, not the actual local value. This is the same a* introduced at the end of Section 7.5 and used in Equation
(8.35) . The value of a* is given by a* = *JyRT*. Let us now obtain a relation between the actual Mach number M and this defined characteristic Mach number M*. Dividing Equation (8.35) by u2, we have
(a/u)2 1 _ у + 1 / a*2
у – 1 2 “ 2(y – 1) V и )
(1/M)2 = y + 1 /J_2 _ 1
у – 1 2(y – 1) M*/ 2
![]() 2 2
2 2
M2 = —————— Z————-
(у + 1 )/M*2 – (у – 1)
Equation (8.47) gives M as a function of M*. Solving Equation (8.47) for M*2, we have
which gives M* as a function of M. As can be shown by inserting numbers into Equation (8.48) (try some yourself),
|
M* = 1 |
if M = 1 |
|
M* < 1 |
if M < 1 |
|
M* > 1 |
if M > 1 |
|
Iy + 1 |
|
|
M* It———– r |
if M —>■ oo |
|
у – 1 |
Therefore, M* acts qualitatively in the same fashion as M except that M* approaches a finite value when the actual Mach number approaches infinity.
In summary, a number of equations have been derived in this section, all of which stem in one fashion or another from the basic energy equation for steady, inviscid, adiabatic flow. Make certain that you understand these equations and become very
2 Foe
[1] Strictly speaking, dA can never achieve the limit of zero, because there would be no molecules at point В in that case. The above limit should be interpreted as dA approaching a very small value, near zero in
terms of our macroscopic thinking, but sufficiently larger than the average spacing between molecules on a microscopic basis.
[3] The specific heat of a fluid is defined as the amount of heat added to a system, Sq, per unit increase in temperature; cv = Sq/dT if Sq is added at constant volume, and similarly, for cp if Sq is added at constant pressure. Specific heats are discussed in detail in Section 7.2. The thermo! conductivity relates heat flux to temperature gradients in the fluid. For example, if qx is the heat transferred in the x direction per second per unit area and aT/ax is the temperature gradient in the x direction, then thermal conductivity к is defined by qx = —k(a = T/ax). Thermal conductivity is discussed in detail in Section 15.3.
[4] Some books do not use the minus sign in the definition of circulation. In such cases, the positive sense of both the line integral and Г is in the same direction. This causes no problem as long as the reader is aware of the convention used in a particular book or paper.
[5] An inviscid, incompressible fluid is sometimes called an ideal fluid, or perfect fluid. This terminology will not be used here because of the confusion it sometimes causes with "ideal gases" or "perfect gases" from thermodynamics. This author prefers to use the more precise descriptor "inviscid, incompressible flow," rother than ideal fluid or perfect fluid.
[6] For a simpler, more rudimentary derivation of Equation (3.21), see chapter 4 of Reference 2. In the present discussion, we have established a more rigorous derivation of Equation (3.21), consistent with the general integral form of the continuity equation.
The above example illustrates two aspects of such a flow, as follows:
[8] Consider a given point on the airfoil surface. The Cp is given at this point and, from the statement of the problem. Cp is obviously unchanged when the velocity is increased from 80 to 300 ft/s. Why? The answer underscores part of our discussion on dimensional analysis in Section 1.7, namely, Cp should depend only on the Mach number, Reynolds number, shape and orientation of the body, and location on the body. For the low-speed inviscid flow considered here, the Mach number and Reynolds number are not in the picture. For this type of flow, the variation of Cp is a function only of location on the surface of the body, and the body shape and orientation. Hence, Cp will not change with or p^ as long as the flow can be considered inviscid and incompressible. For such a flow, once the Cp distribution over the body has been determined by some means, the same Cp distribution will exist for all freestream values of and
[9] In part ib) of Example 3.8, the velocity at the point where Cp is a peak (negative) value is a large value, namely, 753 ft/s. Is Equation (3.38) valid for this case? The answer is essentially no. Equation (3.38) assumes incompressible flow. The
Consider the nonlifting flow over a circular cylinder. Calculate the locations on the surface of the cylinder where the surface pressure equals the freestream pressure.
Solution
When p = pco, then Cp = 0. From Equation (3.101),
Cp = 0 = 1 — 4 sin2 в
Hence, sin# =
Aerodynamics, The Science of Air in Motion, McGraw-Hill, New York, 1982.
[12] For more details, see the interesting discussion on forest aerodynamics in the book by John E. Allen entitled
[13] The design lift coefficient is the theoretical lift coefficient for the airfoil when the angle of attack is such that the slope of the mean camber line at the leading edge is parallel to the freestream velocity.
[14] In many references, such as Reference 1 1, if is common to plot versus С/, rather than versus a. A plot of versus Cj is called a drag polar. For the sake of consistency with Figure 4.5, we choose to plot versus a here.
[15] Kelvin’s theorem also holds for an inviscid compressible flow in the special case where p — p[p); that is, the density is some single-valued function of pressure. Such is the case for isentropic flow, to be treated in later chapters.
[16] fh!2
CDJ = -—- r(y)oCj(y)dy
vcoJ J-b/2











