Stream Function

In this section, we consider two-dimensional steady flow. Recall from Section 2.11 that the differential equation for a streamline in such a flow is given by Equation

 

(2.118), repeated below

dy v dx и

If и and v are known functions of x and y, then to yield the algebraic equation for a streamline:

f(x, y) = c

where c is an arbitrary constant of integration, with different values for different streamlines. In Equation (2.139), denote the function of x and у by the symbol f. Hence, Equation (2.139) is written as

Ф(х, y)=C

The function jr(x, y) is called the stream function. From Equation (2.140) we see that the equation for a streamline is given by setting the stream function equal to a constant, i. e., сі, c2, сз, etc. Two different streamlines are illustrated in Figure 2.38; streamlines ab and cd are given by jr = a and iJr = C2, respectively.

There is a certain arbitrariness in Equations (2.139) and (2.140) via the arbitrary constant of integration c. Let us define the stream function more precisely in order to reduce this arbitrariness. Referring to Figure 2.38, let us define the numerical value of іJr such that the difference AiJr between f = ci for streamline cd and jr = c for streamline ab is equal to the mass flow between the two streamlines. Since Figure 2.38 is a two-dimensional flow, the mass flow between two streamlines is defined per unit depth perpendicular to the page. That is, in Figure 2.38 we are considering the mass flow inside a streamtube bounded by streamlines ab and cd, with a rectangular cross­sectional area equal to An times a unit depth perpendicular to the page. Here, An is the normal distance between ab and cd, as shown in Figure 2.38. Hence, mass flow between streamlines ab and cd per unit depth perpendicular to the page is

Ді/r = C2 — Ci [2.141]

The above definition does not completely remove the arbitrariness of the constant of integration in Equations (2.139) and (2.140), but it does make things a bit more precise. For example, consider a given two-dimensional flow field. Choose one streamline of the flow, and give it an arbitrary value of the stream function, say, fr = a. Then, the value of the stream function for any other streamline in the flow, say, fr = сг,

is fixed by the definition given in Equation (2.141). Which streamline you choose to designate as ф = c and what numerical value you give c usually depend on the geometry of the given flow field, as we see in Chapter 3.

The equivalence between ф = constant designating a streamline, and Аф equal­ing mass flow (per unit depth) between streamlines, is natural. For a steady flow, the mass flow inside a given streamtube is constant along the tube; the mass flow across any cross section of the tube is the same. Since by definition Д ф is equal to this mass flow, then Аф itself is constant for a given streamtube. In Figure 2.38, if ф = C designates the streamline on the bottom of the streamtube, then ф2 = <"2 = c + Аф is also constant along the top of the streamtube. Since by definition of a streamtube (see Section 2.11) the upper boundary of the streamtube is a streamline itself, then ф2 = C2 = constant must designate this streamline.

We have yet to develop the most important property of the stream function, namely, derivatives of ф yield the flow-field velocities. To obtain this relationship, consider again the streamlines a b and cd in Figure 2.38. Assume that these streamlines are close together (i. e., assume An is small), such that the flow velocity V is a constant value across An. The mass flow through the streamtube per unit depth perpendicular to the page is

Аф = pV An(l) Аф

~^=PV

An

Consider the limit of Equation (2.142) as An —» 0:

,, r АФ H

pV = lim ——— = —

An->0 An dn

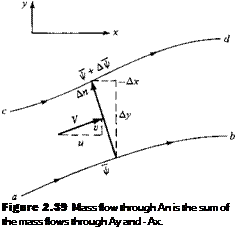
Equation (2.143) states that if we know ф, then we can obtain the product (p V) by differentiating ф in the direction normal to V. To obtain a practical form of Equation (2.143) for cartesian coordinates, consider Figure 2.39. Notice that the directed normal distance An is equivalent first to moving upward in the у direction by the amount Ay and then to the left in the negative x direction by the amount — Ax. Due to conservation of mass, the mass flow through An (per unit depth) is equal to the sum of the mass flows through Ay and — Ax (per unit depth):

Mass flow = Аф = pV An = pu Ay + pv(-Ax) [2.144]

Letting cd approach ab, Equation (2.144) becomes in the limit

d’ijf = pudy — pvdx [2.145]

However, since ф = ф (x, y), the chain rule of calculus states

– 3 ф 3 ф

dф = —dx H——- dy [2.146]

dx dy

Comparing Equations (2.145) and (2.146), we have
[2.147a]

[2.147b]

Equations (2.147a and b) are important. If ф(х, y) is known for a given flow field, then at any point in the flow the products pu and pv can be obtained by differentiating ф in the directions normal to и and v, respectively.

If Figure 2.39 were to be redrawn in terms of polar coordinates, then a similar derivation yields

Such a derivation is left as a homework problem.

Note that the dimensions of ф are equal to mass flow per unit depth perpendicular to the page. That is, in SI units, ф is in terms of kilograms per second per meter perpendicular to the page, or simply kg/(s ■ m).

The stream function ф defined above applies to both compressible and incom­pressible flow. Now consider the case of incompressible flow only, where p = con-

stant. Equation (2.143) can be written as

д(Ф/р)

dn

We define a new stream function, for incompressible flow only, as 1jr = i// /p. Then Equation (2.149) becomes

ЗіIr V = ~ dn

and Equations (2.147) and (2.148) become

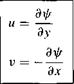[3.150a]

[3.150b]

and

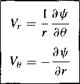[3.151a] [3.151b]

The incompressible stream function ф has characteristics analogous to its more gen­eral compressible counterpart iJr. For example, since ф(х, у) = c is the equation of a streamline, and since p is a constant for incompressible flow, then 1(r{x, y) = ф jp = constant is also the equation for a streamline (for incompressible flow only). In addition, since Д ф is mass flow between two streamlines (per unit depth perpendic­ular to the page), and since p is mass per unit volume, then physically Аф = Ді]r/p represents the volume flow (per unit depth) between two streamlines. In SI units, Аф is expressed as cubic meters per second per meter perpendicular to the page, or simply m2/s.

In summary, the concept of the stream function is a powerful tool in aerodynam­ics, for two primary reasons. Assuming that ф(х, y) [or ф(х, y)[ is known through the two-dimensional flow field, then:

1. ф = constant (or ф = constant) gives the equation of a streamline.

2. The flow velocity can be obtained by differentiating ф (or ф), as given by Equa­tions (2.147) and (2.148) for compressible flow and Equations (2.150) and (2.151) for incompressible flow. We have not yet discussed how ф(х, y) [or ф(х, у)] can be obtained in the first place; we are assuming that it is known. The ac­tual determination of the stream function for various problems is discussed in Chapter 3.