Substantial Derivative

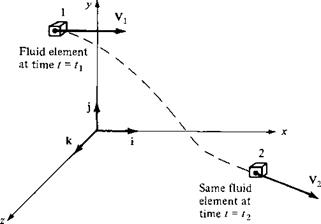
Consider a small fluid element moving through a flow field, as shown in Figure 2.24. This figure is basically an extension of Figure 2.14, in which we introduced the concept of a fluid element moving through a specified flow field. The velocity field is given by V = ui + vj + uik, where

и — u(x, y, z, t) v = v(x, y, z, t) w — w(x, y, z, t)

In addition, the density field is given by

p = p(x, y, z, t)

At time t, the fluid element is located at point 1 in the flow (see Figure 2.24), and its density is

Pi = P(x, Vi, Zi, fi)

Figure 2.24 Fluid element moving in a flow field —illustration for the substantial derivative.

At a later time f2 the same fluid element has moved to a different location in the flow field, such as point 2 in Figure 2.24. At this new time and location, the density of the fluid element is

Pi = P(x2, У2, Z2, tl)

Since p = p{x, у, г, t), we can expand this function in a Taylor series about point 1 as follows:

(Уі ~ Уі) + (Z2 – Z)

ґдр

+ ( — I (h — fi) + higher-order terms dt ) у

Dividing by t2 — t, and ignoring the higher-order terms, we have Pi – Pi / dp x2 x / dp / У2 ~ Уі / dp Z2-Z1 / Эр

t2-t dx)xt2-ti уЗуД V t2 – ft / 3z / ] t2 t 3f/j

[2.101]

Consider the physical meaning of the left side of Equation (2.101). The term (p2 — P)/(h — t) is the average time rate of change in density of the fluid element as it moves from point 1 to point 2. In the limit, as t2 approaches t, this term becomes

p2 – pi Dp

hm ———- = —

h—’t2 — t Dt

Here, Dp/Dt is a symbol for the instantaneous time rate of change of density of the fluid element as it moves through point 1. By definition, this symbol is called the substantial derivative D/Dt. Note that Dp/Dt is the time rate of change of density

of a given fluid element as it moves through space. Here, our eyes are locked on the fluid element as it is moving, and we are watching the density of the element change as it moves through point 1. This is different from (dp/dt), which is physically the time rate of change of density at the fixed point 1. For (dp/dt), we fix our eyes on the stationary point 1, and watch the density change due to transient fluctuations in the flow field. Thus, Dp/Dt and dpjdt are physically and numerically different quantities.

Returning to Equation (2.101), note that

Thus, taking the limit of Equation (2.101) as t2 t, we obtain

	dp dp dz + dt
[3.103]

Examine Equation (2.102) closely. From it, we can obtain an expression for the substantial derivative in cartesian coordinates:

[3.103]

Furthermore, in cartesian coordinates, the vector operator V is defined as

3 3

——- 1- к —

dy dz

Hence, Equation (2.103) can be written as

D Dt

[3.104]

Equation (2.104) represents a definition of the substantial derivative in vector notation; thus, it is valid for any coordinate system.

Focusing on Equation (2.104), we once again emphasize that D/Dt is the sub­stantial derivative, which is physically the time rate of change following a moving fluid element; 3/31 is called the local derivative, which is physically the time rate of change at a fixed point; V • V is called the convective derivative, which is physically the time rate of change due to the movement of the fluid element from one location to another in the flow field where the flow properties are spatially different. The sub­stantial derivative applies to any flow-field variable, e. g., Dp/Dt, DT/Dt, Du/Dt. For example,

DT З T dT dT d T dT

—– =——— b (V • V)T =——— f – и——- b V—— b w —

Dt dt dt dx dy dz

local comcclive

derivative derivative

Again, Equation (2.105) states physically that the temperature of the fluid element is changing as the element sweeps past a point in the flow because at that point the flow-field temperature itself may be fluctuating with time (the local derivative) and because the fluid element is simply on its way to another point in the flow field where the temperature is different (the convective derivative).

Consider an example which will help to reinforce the physical meaning of the substantial derivative. Imagine that you are hiking in the mountains, and you are about to enter a cave. The temperature inside the cave is cooler than outside. Thus, as you walk through the mouth of the cave, you feel a temperature decrease—this is analogous to the convective derivative in Equation (2.105). However, imagine that, at the same time, a friend throws a snowball at you such that the snowball hits you just at the same instant you pass through the mouth of the cave. You will feel an additional, but momentary, temperature drop when the snowball hits you—this is analogous to the local derivative in Equation (2.105). The net temperature drop you feel as you walk through the mouth of the cave is therefore a combination of both the act of moving into the cave, where it is cooler, and being struck by the snowball at the same instant—this net temperature drop is analogous to the substantial derivative in Equation (2.105).