Supersonic Altitude Stability

A somewhat strange lack of stability cropped up when airplanes began to operate at supersonic speeds above about Mach 2 at quite high altitudes. This showed up as an inability to control altitude and airspeed precisely in flights of the North American XB-70 Valkyrie and the Lockheed SR-71A. The Concorde SST with a maximum speed around Mach 2 is believed to have difficulties of this sort, as well. According to Glenn B. Gilyard and John W. Smith (1978), on the SR-71A:

Decreased aircraft stability, low static pressures, and the presence of atmospheric distur­bances are all factors that contribute to this degraded control. The combination of high altitude and high speed also contributes to an unfavorable balance between kinetic and po­tential energy, thereby requiring large altitude changes to correct for small Mach number errors when flying a Mach hold mode using the elevator control.

In simulating SR-71A supersonic altitude and airspeed control problems NASA found it necessary to add to the normal equations of aircraft motion inlet geometry effects on airplane motion, inlet operating characteristics up to the unstart boundary, and the afterburning equations for the two engines. While with these additions simulation presents no unusual difficulties, attempts to find suitable theoretical models are another matter.

The applicable body of theory begins with Lanchester’s 1897 analysis of phugoid mo­tion. Lanchester’s model, and the Bryan and Williams analyses that followed, neglected atmospheric density changes as an airplane’s height changes during a longitudinal oscilla­tion. F. N. Scheubel added density gradient to the mathematical model in 1942. In 1950, Stefan Neumark added the effects of thrust and sound speed variations with altitude to the equations.

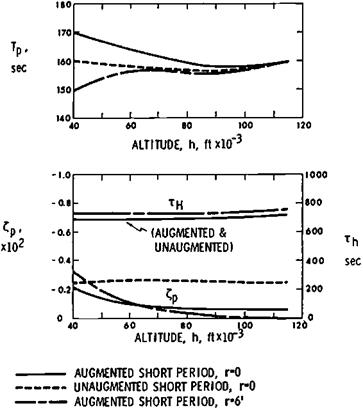
While the classical Bryan-Williams model leads to a fourth-degree characteristic equa­tion, with both short – and long-period longitudinal oscillations, density gradient increases the characteristic equation degree to 5. A new aperiodic height mode appears, typically a very slow divergence (Figure 11.16). The height mode was first identified, or rather predicted, by Neumark. The supersonic altitude stability problems thus far encountered probably involve both the phugoid or long-period mode and the height mode.

Thrust effects are significant on both the phugoid and height modes (Stengel, 1970; Sachs, 1990). Aside from the effects of possible thrust offsets from the airplane’s center of gravity, the throttle-fixed variation in thrust with airspeed affects both the phugoid and height modes. Both modes are stabilized when thrust decreases with increasing airspeed, and vice versa.

Lanchester’s original analysis (Durand, 1934) assumes an airplane whose lift is always at right angles to the flight path and numerically proportional to the square of the airspeed. These simple assumptions and small-angle approximations lead to Lanchester’s phugoid motion, an undamped oscillation of period ^2n V/g, where V is the flight velocity and g is the acceleration of gravity.

Figure 11.16 Effect of altitude on the phugoid and height modes of a hypothetical SST, cruising at a Mach number of 3.0. (From Stengel, Jour of Aircraft, Sept.-Oct. 1970)

However, the linear increase of period with airspeed predicted by Lanchester does not occur at high airspeeds. The reason is that the density gradient effect that Scheubel wrote about in 1942 becomes very important at high airspeeds. The phugoid period is shortened compared with the Lanchester case. In effect, as the airplane noses down, picking up speed and giving up potential energy for kinetic energy, higher density at the lower altitude increases lift, bending the path upward again. Higher density at lower altitudes acts as an extra spring, shortening the period.

A simplified model developed in 1965 by Lockheed’s John R. McMaster predicts drastic reductions in the phugoid period relative to the classic Lanchester values at high airspeeds. McMaster’s predicted period at a Mach number of 3.0 is about 150 seconds, compared with the Lanchester value of 401 seconds. Calculations by Stengel in 1970 for an SST configuration at a Mach number of 3.0 give a phugoid period of about 160 seconds, close to the McMaster value. A later simplified model (Etkin, 1972) shows a reduction from the Lanchester values, but not quite so large.

A formulation by Regan (1993) also corrects the Lanchester approximation for density gradient. Regan’s approximation may be derived from the small-perturbation longitudinal equations of motion of Figure 18.4 by adding a height degree of freedom and the height derivative dZ/dh, where Z is the Z-axis aerodynamic force and h is altitude perturbation from equilibrium flight. The Regan approximation for phugoid period is

Mach number

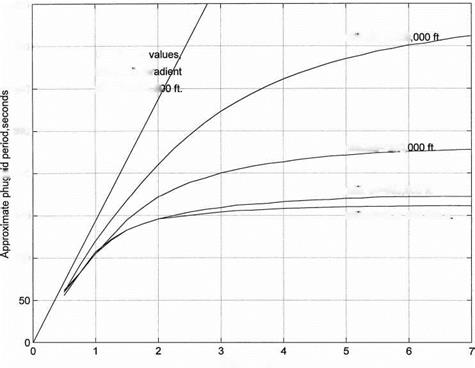
Figure 11.17 Variation of approximate phugoid period with altitude and Mach number, including density gradient with height effects.

Period = 2ж(V0/g)/(2 – (1/p)(dp/dh)(Vo/g))1/2,

where V0 = equilibrium flight speed,

p = equilibrium air density,

g = acceleration of gravity at the equilibrium altitude,

dp/dh = density gradient with altitude at the equilibrium altitude.

This relationship is used to show the general trend of phugoid period with Mach number and altitude in Figure 11.17. Omitted are possible thrust effects. Figure 11.17 shows that density gradient causes the phugoid period to reach asymptotic values as airspeed increases indefinitely, which is at odds with the classical Lanchester approximation. Neglect of density gradient incorrectly doubles the approximated phugoid period at an altitude of 200,000 feet and Mach number = 2.

Figure 11.17 predicts a phugoid period of 154 seconds at Mach 3 at altitudes below 400,000 feet. This is close to McMaster’s predicted value for Mach number 3 and also to Stengel’sresultsin Figure 11.16. Eigenvalue calculationsfor the NASA GHAME hypersonic vehicle give remarkably close results to the Regan approximation for the phugoid period at Mach numbers above 2.

Flight test data that would support one simplified phugoid model or another seem not to be available, for good reason. Typically, airplanes are flown at those very high Mach numbers and altitudes with either or both altitude and Mach hold control loops active, as a direct result of the altitude stability problem. Loop closures modify the basic phugoid

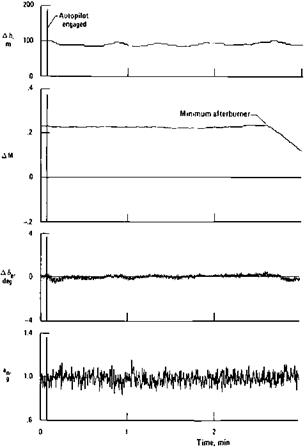
Figure 11.18 YF-12A altitude hold performance with an optimized autopilot, at Mach 3, altitude 77,500 feet. Altitude oscillation about the desired value is held to within plus or minus 25 feet. (From Gilyard and Smith, NASA CP 2054, 1978)

motion to the point where its period and damping would be difficult to detect, even if tests could be devised to measure periods as long as 160 seconds.

NASA flight tests of the YF-12A are encouraging in that properly designed and com­pensated altitude and Mach hold systems, working through the pitch and thrust controls, respectively, seem to be able to hold reasonably stable cruise conditions at Mach 3 (Figure 11.18). One physical limitation is instability in the atmosphere itself, notably tem­perature shears that change the indicated Mach number even though the true airspeed and altitude have not changed. Gilyard and Smith noted that baseline YF-12A altitude hold mode operation varied from day to day. “Occasionally altitude could be held reasonably constant; at other times, it diverged in an unacceptable manner.”

A related phenomenon was found in flight testing the XB-70 around a Mach number of 3. Indicated altitude changes of 1,000 feet were seen in 2 or 3 seconds, quite evidently the result of atmospheric temperature gradients, since the airplane could not have possibly changed altitude so quickly. To avoid having altitude and Mach hold systems chase after atmospheric instabilities, it may be necessary to smooth atmospheric data with inertial data or position measurements derived from satellites.