Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Swept wings
When an aircraft approaches the speed of sound, the flow begins to change to the supersonic type described in Chapter 5. Although it is possible to accommodate the consequences of these changes, it is difficult to design a wing that behaves well in both low speed and supersonic flow. Even if the lift and drag
|
Fig. 2.16 The BERP-tip helicopter blade tip In high speed flight, the retreating blade has to operate at a high angle of attack. This tip design produces separated conical vortex flow, inhibiting tip stalling. The increased chord at the tip lowers the thickness-to-chord ratio, which reduces compressibility effects on the advancing blade, when the relative velocity approaches the speed of sound |
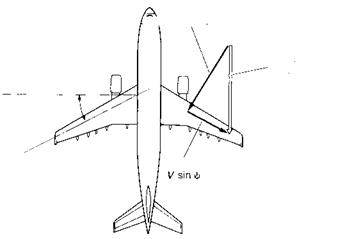
Normal component
СЛ V cos ili
Free-stream velocity V (= aircraft speed)
Sweep angle ф
Spanwise component
Fig. 2.17 Velocity components on a swept wing
Only the normal component contributes to the generation of lift properties are acceptable, the change of flow drastically alters the handling, control and stability characteristics. Difficulties occur particularly at transition from one type of flow to the other.
One way to reduce these problems, is to sweep the wings backwards, or less commonly forwards. As illustrated in Fig. 2.17, the air flow may be considered as having two components of velocity, one at right angles or normal to the span (the normal component), and one along the direction of the span (the spanwise component). The spanwise component does not alter much as the flow passes over the wing, and changes of speed occur mainly in the normal component. If
the angle of sweep is sufficient, the normal component of velocity can be slower than the speed of sound even when the aircraft is flying faster than the speed of sound.
If we look at the flow past a section of a swept wing, we will see that as long as the normal component is less than the speed of sound (subsonic), the flow patterns and general flow features are similar to those for ordinary low speed flow. This is true even though the resultant of the normal and spanwise components of velocity may be supersonic in places. The explanation for this is given in Chapter 8.
The normal component of velocity is roughly equal to the relative air speed multiplied by the cosine of the angle of sweep. It follows that the amount of sweep required increases with increasing aircraft maximum speed.
Even if an aircraft is not intended to be flown faster than the speed of sound, the wings may need to be swept, since the air flow may become supersonic locally, particularly on the upper surface, where it is moving faster than the free stream (the approaching flow). This can occur at flight speeds of around 60 to 70 per cent of the speed of sound, and since medium and long-haul airliners nowadays fly faster than this, they invariably have swept wings.
The idea of using wing sweep was developed by a group of German engineers including A. Betz, at around the time of the outbreak of the Second World War. The first successful operational jet aircraft, the Messerschmitt Me-262 (Fig. 2.18)
|
Fig. 2.18 German engineers were aware of the advantages of wing sweep, which was used on Messerschmitt Me-262; the first jet aircraft to enter active service (in 1944) |
used a modest amount of sweep. Allied wartime jet aircraft, such as the Gloster Meteor, which were designed without the benefit of Betz’s theories, used unswept wings. After the war, when the information became available, many designs were hurriedly changed. The straight-winged Supermarine Attacker design was developed to produce the swept-wing Swift.
