The Aerodynamic Center: Additional Considerations

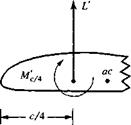
The definition of the aerodynamic center is given in Section 4.3; it is that point on a body about which the aerodynamically generated moment is independent of angle of attack. At first thought, it is hard to imagine that such a point could exist. However, the moment coefficient data in Figure 4.6, which is constant with angle of attack, experimentally proves the existence of the aerodynamic center. Moreover, thin airfoil theory as derived in Sections 4.7 and 4.8 clearly shows that, within the assumptions embodied in the theory, not only does the aerodynamic center exist but that it is located at the quarter-chord point on the airfoil. Therefore, to Figure 1.19 which illustrates three different ways of stating the force and moment system on an airfoil, we can now add a fourth way, namely, the specification of the lift and drag acting through the aerodynamic center, and the value of the moment about the aerodynamic center. This is illustrated in Figure 4.23.

Figure 4.23 Lift, drag, and moments about the aerodynamic center.

Figure 4.24 Lift and moments about the quarter-chord point, and a sketch useful for locating the aerodynamic center.

For most conventional airfoils, the aerodynamic center is close to, but not neces­sarily exactly at, the quarter-chord point. Given data for the shape of the lift coefficient curve and the moment coefficient curve taken around an arbitrary point, we can calcu­late the location of the aerodynamic center as follows. Consider the lift and moment system taken about the quarter-chord point, as shown in Figure 4.24. We designate the location of the aerodynamic center by ciac measured from the leading edge. Here, xac is the location of the aerodynamic center as a fraction of the chord length c. Taking moments about the aerodynamic center designated by ac in Figure 4.24, we have

M’c = L'(cxac – cl A) + M’c/4 Dividing Equation (4.67) by q^Sc, we have

or	[4.68]
„ dci dcmcj 4 0 = — (xac – 0.25) H——— —-L- da da
[4.70]
For airfoils below the stalling angle of attack, the slopes of the lift coefficient and

moment coefficient curves are constant. Designating these slopes by

Equation (4.70) becomes

0 = a0(*ac – 0.25) + m0

Hence, Equation (4.71) proves that, for a body with linear lift and moment curves, that is, where ao and mo are fixed values, the aerodynamic center exists as a fixed point on the airfoil. Moreover, Equation (4.71) allows the calculation of the location of this point.

Consider the NACA 23012 airfoil studied in Example 4.2. Experimental data for this airfoil is plotted in Figure 4.22, and can be obtained from Reference 11. It shows that, at a = 4°, с-; = 0.55 and c„, t/4 = —0.005. The zero-lift angle of attack is —1.1°. Also, at a = —4°, cm cj4 = —0.0125. (Note that the “experimental” value of cmx/4 = —0.01 tabulated at the end of Example 4.2 is an average value over a range of angle of attack. Since the calculated value of 4 from thin airfoil theory states that the quarter-chord point is the aerodynamic center, it makes sense in Example 4.2 to compare the calculated c,„ ,./4 with an experimental value averaged over a range of angle of attack. However, in the present example, because c„,,( /4 in reality varies with angle of attack, we use the actual data at two different angles of attack.) From the given information, calculate the location of the aerodynamic center for the NACA 23012 airfoil.

Solution

Since ci = 0.55 at a = 4° and q = 0 at a = —1.1°, the lift slope is

The slope of the moment coefficient curve is

From Equation (4.71),

The result agrees exactly with the measured value quoted on page 183 of Abbott and Von Doenhoff (Reference 11).