The boundary layer and high speed flow

In the above section we saw that, in supersonic flow as well as subsonic, boundary layers exist and can separate. There is a great deal of similarity in the behaviour of the boundary layer at both high and low speeds. Chapter 3 is applicable above as well as below the speed of sound. The requirement that the flow is at rest relative to the surface (the no-slip condition) is still applic­able and so somewhere in the boundary layer the flow goes from subsonic to supersonic speed (Fig. 5.20).

A Local velocity is zero В Local velocity = speed of sound C Local velocity = 99% external velocity Fig. 5.20 Sonic line in supersonic boundary layer Even at supersonic speeds the velocity still falls to zero at the surface at the bottom of the boundary layer

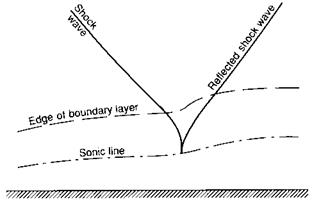
Fig. 5.21 Shock wave reflection at surface Shock wave does not reach surface because flow at the bottom of the boundary layer is subsonic

One way in which the boundary layer in supersonic flow can be subjected to a severe pressure gradient is when a shock wave, which may be generated by another part of an aircraft, strikes the surface. In this case the shock wave reflects as is shown in Fig. 5.21. It will be observed that the shock wave cannot penetrate right to the surface but only as far as the sonic line (see Fig. 5.21), but the pressure rise is transmitted through the boundary layer and may well cause separation to occur.

Figure 5.21 shows that the reflection process is quite complex. As the flow speed falls within the boundary layer so the shock wave angle becomes steeper to give the same pressure rise, as the local Mach number is reduced. The increase in pressure in the boundary layer will cause it to thicken and may well cause separation. The picture shown in Fig. 5.21 is therefore just one of a number of possibilities.

It should be noted that we have been guilty of some simplification in some of the previous figures. For example the shock wave in Fig. 5.12 has been drawn right down to the surface as if there were no boundary layer present. This may be an acceptable approximation in many cases, but if the boundary layer should separate then the picture may be changed considerably.

Shock wave reflections of this sort are important in determining how the flow behaves, and reflections are by no means always as simple as that shown in Fig. 5.21. The boundary layer at the point of reflection as well as the strength of the shock wave may be complicated by such factors as local separation bubbles or complete boundary layer separation. Three­dimensional effects will also have an important bearing on the nature of the reflection process. A detailed discussion of the various types of reflection which may be encountered is outside the scope of this book, and the interested reader will find a great deal on the subject in the literature, e. g. Cox and Crabtree (1965).

Kinetic heating

In Chapter 2 we saw how the pressure and velocity for a low speed flow could be related by Bernoulli’s equation. This equation is only approximately true, however, and, for a compressible fluid, becomes less accurate as the speed of flow increases. This is because significant changes start to occur not only in the kinetic energy of the fluid but also in the internally stored energy within the gas. This means that, as the speed increases, not only does the pressure fall but so does the temperature. Conversely, when a high speed air stream is slowed down there is an accompanying rise in the temperature.

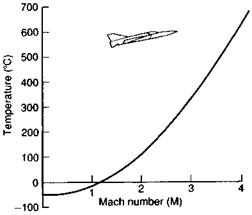
Again it makes no difference if we consider the aircraft moving through the air rather than the air streaming past the stationary aircraft. The rise in tem­perature is most severe when the air is brought to rest, relative to the aircraft, at a stagnation point. Figure 5.22 shows the air temperatures encountered, at different flight Mach numbers, in such a stagnation region at a cruising height roughly equivalent to that of Concorde. Such temperature rises can have important implications in terms of structural strength and distortion.

We have seen that another way in which the air can be suddenly slowed in supersonic flow is by the presence of a shock wave. Frequently very severe heating problems can be encountered where the flow passes through a local shock wave near the surface. One example of this is provided by the high local heating rates which can occur at a junction between a fin and a fuselage.

The boundary layer provides another mechanism which can raise the air temperature with important structural consequences for high speed aircraft. The boundary layer slows the flow near the surface with a consequential

Fig. 5.22 Variation of stagnation temperature with flight Mach number at high altitude above 11 km

temperature rise. This temperature increase is only of any significance at high flight speeds.

The state of the boundary layer is also important in determining the rate of heat transfer to the surface. In general a turbulent boundary layer will transmit heat into the structure more readily than a laminar layer because in the turbu­lent layer the regions of the boundary layer close to the surface are continually replenished with high temperature air.

This heat transfer process can also affect the way in which the boundary layer behaves. The extreme temperatures which may be encountered at very high (hypersonic) speed may cause significant changes in the properties of the air itself, as we shall discuss briefly in the next section.