The Cambered Airfoil

Thin airfoil theory for a cambered airfoil is a generalization of the method for a symmetric airfoil discussed in Section 4.7. To treat the cambered airfoil, return to Equation (4.18):

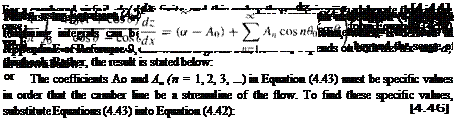
Recall that Equation (4.46) was obtained directly from Equation (4.42), which is the transformed version of the fundamental equation of thin airfoil theory, Equa­tion (4.18). Furthermore, recall that Equation (4.18) is evaluated at a given point, r along the chord line, as sketched in Figure 4.19. Hence, Equation (4.46) is also eval­uated at the given point x; here, dz/dx and во correspond to the same point л: on the chord line. Also, recall that dz/dx is a function of во, where л: = (c/2)(l — cos0o) from Equation (4.21).

Examine Equation (4.46) closely. It is in the form of a Fourier cosine series ex­pansion for the function of dz/dx. In general, the Fourier cosine series representation of a function f (в) over an interval 0 < в < ж is given by

OO

/((9) = B0 + Bn cos пв [4.47]

n=I

where, from Fourier analysis, the coefficients Bo and Bn are given by

Bo = – f f (в) dO [4.48]

л Jo

2 Г

and Bn — — / f {6)cosn6 d6 [4.49]

л – Jo

(See, e. g., page 217 of Reference 6.) In Equation (4.46), the function dz/dx is analo­gous to f(6) in the general form given in Equation (4.47). Thus, from Equations (4.48) and (4.49), the coefficients in Equation (4.46) are given by

	1 Г dz a – A0 = — —dOо Jr Jo dx
or	1 [л dz Ao = a—— / — dOo Jr Jo dx	[4.50]
and	2 Cn dz An = — / — cos пво dOо n Jo dx	[4.51]

Keep in mind that in the above, dz/dx is a function of в0. Note from Equation (4.50) that Ao depends on both a and the shape of the camber line (through dz/dx), whereas from Equation (4.51) the values of An depend only on the shape of the camber line.

Pause for a moment and think about what we have done. We are considering the flow over a cambered airfoil of given shape dz/dx at a given angle of attack a. In order to make the camber line a streamline of the flow, the strength of the vortex sheet along the chord line must have the distribution у (в) given by Equation (4.43), where the coefficients A0 and An are given by Equations (4.50) and (4.51), respectively. Also, note that Equation (4.43) satisfies the Kutta condition y(n) = 0. Actual numbers for Ao and An can be obtained for a given shape airfoil at a given angle of attack simply by carrying out the integrations indicated in Equations (4.50) and (4.51). For an example of such calculations applied to an NACA 2412 airfoil, see pages 120­125 of Reference 13. Also, note that when dz/dx = 0, Equation (4.43) reduces to Equation (4.24) for a symmetric airfoil. Hence, the symmetric airfoil is a special case of Equation (4.43).

Let us now obtain expressions for the aerodynamic coefficients for a cambered airfoil. The total circulation due to the entire vortex sheet from the leading edge to the trailing edge is

Г= f y(^)d^=C – [ y(0)sm0de JO ^ Jo

[4.53]

and

Hence, Equation (4.53) becomes

Г — cVqo (ttAq +

From Equation (4.54), the lift per unit span is L — Poo 1^00 Г — Рсо^оо^ (жА0 3“ In turn, Equation (4.55) leads to the lift coefficient in the form L’

[4.55]

[4.56]

ci

Recall that the coefficients A0 and A i in Equation (4.56) are given by Equations (4.50) and (4.51), respectively. Hence, Equation (4.56) becomes

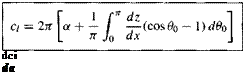[4.57]

and	Lift slope =	[4.58]
— 2tz

Equations (4.57) and (4.58) are important results. Note that, as in the case of the symmetric airfoil, the theoretical lift slope for a cambered airfoil is 2jt. It is a general result from thin airfoil theory that dci/da = 2jt for any shape airfoil. However, the expression for c; itself differs between a symmetric and a cambered airfoil, the difference being the integral term in Equation (4.57). This integral term has physical significance, as follows. Return to Figure 4.4, which illustrates the lift curve for an airfoil. The angle of zero lift is denoted by <xl=q and is a negative value. From the geometry shown in Figure 4.4, clearly

dci, ,

ci = — (a – aL=Q) da

Substituting Equation (4.58) into (4.59), we have

ci = 2n{a — aL=o) [4.60]

Comparing Equations (4.60) and (4.57), we see that the integral term in Equa­tion (4.57) is simply the negative of the zero-lift angle; that is

[4.61]

Hence, from Equation (4.61), thin airfoil theory provides a means to predict the angle of zero lift. Note that Equation (4.61) yields aL=o = 0 for a symmetric airfoil, which is consistent with the results shown in Figure 4.20. Also, note that the more highly cambered the airfoil, the larger will be the absolute magnitude of c/l=o-

Returning to Figure 4.21, the moment about the leading edge can be obtained by substituting у (в) from Equation (4.43) into the transformed version of Equa­tion (4.35). The details are left for Problem 4.9. The result for the moment coefficient is

Аг ~2

[4.62]

Substituting Equation (4.56) into (4.62), we have

Г сі n і Cm, le = — 1^— + ~(Al ~ A2)J

[4.63]

Note that, for dz/dx = 0, A = Аг = 0 and Equation (4.63) reduces to Equa­tion (4.39) for a symmetric airfoil.

The moment coefficient about the quarter chord can be obtained by substituting Equation (4.63) into (4.40), yielding

[4.64]

Cm, с/4 — ^ (Аг A])

Unlike the symmetric airfoil, where ст с/4 = 0, Equation (4.64) demonstrates that cm, c/4 is finite for a cambered airfoil. Therefore, the quarter chord is not the center of pressure for a cambered airfoil. However, note that A1 and Аг depend only on the shape of the camber line and do not involve the angle of attack. Hence, from Equation (4.64), сш, с/4 is independent of a. Thus, the quarter-chord point is the theoretical location of the aerodynamic center for a cambered airfoil.

The location of the center of pressure can be obtained from Equation (1.21):

Cm, leC

u

[4.66]

Equation (4.66) demonstrates that the center of pressure for a cambered airfoil varies with the lift coefficient. Hence, as the angle of attack changes, the center of pressure also changes. Indeed, as the lift approaches zero, xcp moves toward infinity; that is, it leaves the airfoil. For this reason, the center of pressure is not always a convenient point at which to draw the force system on an airfoil. Rather, the force-and-moment system on an airfoil is more conveniently considered at the aerodynamic center. (Re­turn to Figure 1.19 and the discussion at the end of Section 1.6 for the referencing of the force-and-moment

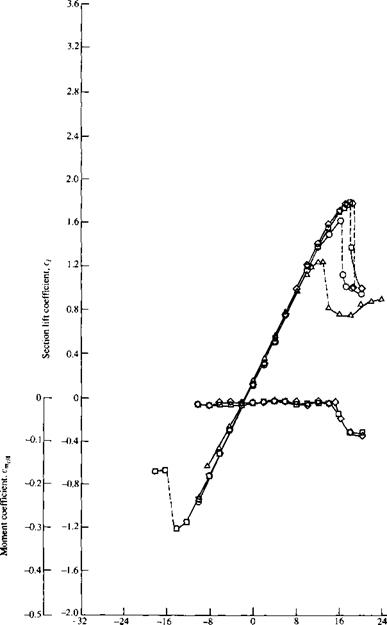
Section angle of attack a, degree Figure 4.33 Lift – and moment-coefficient data for an NACA 23012 airfoil, for comparison with the theoretical results obtained in Example 4.2.

Note that the results from thin airfoil theory for a cambered airfoil agree very well with the experimental data. Recall that excellent agreement between thin airfoil theory for a symmetric airfoil and experimental data has already been shown in Figure 4.20. Hence, all of the work we have done in this section to develop thin airfoil theory is certainly worth the effort. Moreover, this illustrates that the development of thin airfoil theory in the early 1900s was a crowning achievement in theoretical aerodynamics and validates the mathematical approach of replacing the chord line of the airfoil with a vortex sheet, with the flow tangency condition evaluated along the mean camber line.

This brings to an end our introduction to classical thin airfoil theory. Returning to our road map in Figure 4.2, we have now completed the right-hand branch.