The eN Method

In this section we offer a more detailed presentation of the eN method, because it forms the basis for low Reynolds number aerodynamics predictions and has proven to be useful for engineering applications. As already mentioned, the eN method is based on linear stability analysis, which states that transition occurs when the most unstable TS wave in the boundary layer has been amplified by a certain factor. Given a velocity profile, one can determine the local disturbance growth rate by solving the Orr-Sommerfeld eigenvalue equations. Then, the amplification factor is calculated by integrating the growth rate, usually the spatial growth rate, starting from the point of neutral stability. The Transition Analysis Program System (TAPS) by Wazzan and co-workers [125] and the COSAL program by Malik [126] can be used to compute the growth rate for a given velocity profile. Schrauf also developed a program called Coast3 [127]. However, it is very time consuming to solve the eigenvalue equations. An alternative approach was proposed by Gleyzes et al. [128], who found that the integrated amplification factor n can be approximated by an empirical formula as follows:

dn

n= (H)[Ree – Ree(H)], (2-12)

dRee o

where Ree is the momentum thickness Reynolds number, Ree is the critical Reynolds number that we define later, and H is the shape factor previously discussed. With this approach, one can approximate the amplification factor with a reasonably good accu­racy without solving the eigenvalue equations. For similar flows, the amplification factor n is determined by the following empirical formula:

dn

= 0.01{[2.4H – 3.7 + 2.5 tanh (1.5H – 4.65)]2 + 0.25}1/2. (2-13)

dR. ee

For non-similar flows (i. e., those that cannot be treated by similarity variables using the Falkner-Skan profile family [129]) the amplification factor with respect to the spatial coordinate f is expressed as

dn = dn 1/ f due Л Pиев21

df dReg 2 ue df uef в

An explicit expression for the integrated amplification factor then becomes

f dn

n (f) = — df, (2-15)

fo df

where f0 is the point where Ree = Ree, and the critical Reynolds number is expressed

eo

by the following empirical formulas:

/1415 / 20 3 295

log10Reeo = [HZTi – 0.489J tanh —— – 12.9 j + H-j + 0.44. (2-16)

Once the integrated growth rate reaches the threshold N, flow becomes turbulent. To incorporate the free-stream turbulence level effect, Mack [130] proposed the following correlation between the free-stream intensity 7) and the threshold N:

N = -8.43 – 2.4 1п(7), 0.0007 < Ti < 0.0298. (2-17)

However, care should be taken in using such a correlation. The free-stream tur­bulence level itself is not sufficient to describe the disturbance, and other information, such as the distribution across the frequency spectrum, should also be considered. The so-called receptivity – how the initial disturbances within the boundary layer are related to the outside disturbances – is a critically important issue. Actually, we can only determine the N factor if we know the “effective 7),” which can be defined only through a comparison of the measured transition position with calculated amplifica­tion ratios [131].

A typical procedure to predict the transition point using coupled RANS equa­tions and the eN method is as follows. First, solve the Navier-Stokes equations together with a turbulence model without invoking the turbulent production terms, for which the flow is essentially laminar; then integrate the amplification factor n based on Eq. (2-12) along the streamwise direction; once the value reaches the threshold N, the production terms are activated for the post-transition computa­tions. After the transition point, flow does not immediately become fully turbulent;

instead, the movement toward full turbulence is a gradual process. This process can be described with an intermittency function, allowing the flow to be represented by a combination of laminar and turbulent structures. With the intermittency function, an effective eddy viscosity is used in the turbulence model and can be expressed as follows:

vTe = Y VT,

where y is the intermittency function and vTe is the effective eddy viscosity.

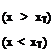In the literature a variety of intermittency distribution functions have been pro­posed. For example, Cebeci [132] presented such a function by improving a model previously proposed by Chen and Thyson [133] for the Reynolds number range of 2.4 x 105 to 2 x 106 with an LSB. However, no model is available when the Reynolds number is lower than 105. Lian and Shyy [117] suggested that, for separation-induced transition at such a low Reynolds number regime, the intermittency distribution is largely determined by the distance from the separation point to the transition point: the shorter the distance, the quicker the flow becomes turbulent. In addition, previ­ous work suggested that the flow property at the transition point is also important. From the available experimental data and our simulations, Lian and Shyy [117] proposed the following model:

where xT is the transition onset position, xS is the separation position, HT is the shape factor at the transition point, and ReeT is the Reynolds number based on the momentum thickness at the transition point.