The generation of lift

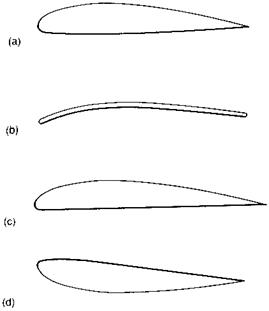
For any aircraft wing, conventional or otherwise, lift is generated by producing a greater pressure under the wing than above it. To produce this pressure difference, all that is required is a surface that is either inclined to the relative air flow direction as shown in Fig. 1.4, or curved (cambered) as in Fig. 1.5. In practice, it is normal to use a combination of inclination and camber. The cross-sectional profiles shown in Figs 1.4 and 1.5 have all been used on suc­cessful aircraft. The shape used for a particular aircraft depends mainly on its speed range and other operational requirements.

The problem is to explain why such shapes produce a pressure difference when moved through the air. Early experimenters found that whether they used a curved or an inclined surface, the average speed of air flow relative to the wing was greater on the upper surface than on the underside. As we shall see later, increases in air flow speed are associated with a reduction in pressure, so the lower pressure on the upper surface is associated with the higher relative air speed. Explanations for the generation of lift are, therefore, often based on the idea that the difference in speed between upper and lower surfaces causes the difference in pressure, which produces the lift. These explanations are, however, unconvincing, because, as with the chicken and the egg, we might alternatively argue that the difference in pressure causes the difference in speed. It is also difficult to explain in simple physical terms why the difference in speed occurs.

One popular and misleading explanation refers to a typical cambered wing section profile such as that shown in Fig. 1.5(a). It is argued, that the air that takes the longer upper-surface route has to travel faster than that which takes the shorter under-surface route, in order to keep up.

Apart from the fact that it is not obvious why the flows over the upper and lower surfaces should have to keep in step, this explanation is unsatisfactory. Inclined flat-plate, or symmetrical-section wings, where the upper and lower

surfaces are the same length, lift just as well as cambered (curved) ones. Also, the cambered profile of Fig. 1.5(a) will still lift even if turned upside down, as in Fig. 1.5(d), as long as it is inclined to the flow direction. Anyone who has ever watched a flying display will be aware that many aircraft can be flown upside down. In fact, there is no aerodynamic reason why any aircraft cannot be flown inverted. The restrictions imposed on this kind of manoeuvre are mainly due to structural considerations.

Almost any shape will generate lift if it is either cambered or inclined to the flow direction. Even a brick could be made to fly by inclining it and propelling it very fast. A brick shape is not the basis for a good wing, but this is mainly because it would produce a large amount of drag in relation to the amount of lift generated.

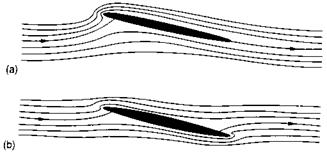
If you study the flow around any of the inclined or cambered sections illus­trated in Figs 1.4 and 1.5, you will find that the air always does go faster over the upper surface. Furthermore, it does take a longer path over the top surface. The unexpected way in which it contrives to do this is shown in Fig. 1.6(a) (and Fig. 1.13). It will be seen that the flow divides at a point just under the nose or leading edge, and not right on the nose as one might have expected. The air does not take the shortest possible path, but prefers to take a rather tortuous route over the top, even flowing forwards against the main stream direction for a short distance.

It is clear that the generation of lift does not require the use of a conven­tional aerofoil section of the type shown in Fig. 1.5(a), and any explanation entirely based on its use is unsatisfactory.

We find that the production of lift depends, rather surprisingly, on the vis­cosity or stickiness of air. Early theories that ignored the viscosity, predicted that the flow patterns around a simple inclined surface would take the form illustrated in Fig. 1.6(b). You will see that in this diagram, there is a kind of symmetry to the pattern of streamlines. They would look exactly the same if you turned the page upside-down. There is, therefore, a similar symmetry in the pressure distribution, so that there must be exactly corresponding areas of low and high pressure on the upper and lower surfaces. Consequently, no lift would be produced.

In reality, the flow patterns are like those shown in Fig. 1.6(a). The import­ant difference is that here the upper and lower surface flows rejoin at the trailing edge, with no sudden change of direction. There is no form of sym­metry in the flow. There is a difference in the average pressure between upper and lower surfaces, and so lift is generated.

This feature of the flows meeting at the trailing edge is known as the Kutta condition. In Chapter 3 we describe how the viscosity (the stickiness) of the air causes this asymmetrical flow, and is thus ultimately responsible for the production of lift.