The inertia forces increase the loads on the main rotor blades

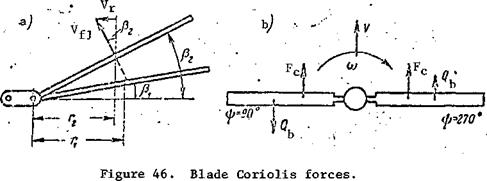
Blade Coriolis forces. In addition to the centrifugal forces and the flapping motion inertial forces, there are the rotational inertia forces, or Coriolis forces. They arise as a result of combination of the circular blade motion and blade motion relative to the horizontal hinge axis (flapping motion). As a result of variation of the flapping angle during flapping motions, there is a change of the radius of the circle along which the blade center of gravity travels. Thus, Figure 46a shows that with increase of the flapping angle from 8^ to the radius of the circle described by the blade center of gravity decreases from r^ to r^. Therefore, the flapping motions

are associated with radial displacement of the blade mass, and this leads to the development of an inertial force which is termed the Coriolis or rotational force.

The essence of the Coriolis force is easily explained if we recall the /62 nature of inertial forces in the case of rectilinear acceleration of motion. Everyone knows from his own experience that during braking the inertia force is directed forward, and that during rectilinear acceleration it is directed aft. Let us apply this rule to the moving blade.

When upward flapping takes place, the radius of the blade center of gravity decreases, and the circumferential velocity decreases, i. e., retardation of the motion takes place, and an inertial force appears which is directed forward in the direction of rotation of the main rotor.

During downward flapping the radius of the circle along which the blade center of gravity travels increases, the circumferential velocity u = cor increases, and an inertial force directed aft — opposite the rotor rotation — appears.

This analysis is confirmed by the energy conservation law and the associated angular momentum conservation law

m^ur = const

where is the mass of the body;

u is the circumferential velocity; r is the trajectory radius of curvature.

Let us apply this law to blade motion during variation of the flapping angle.

Since the power supplied to the main rotor shaft remains constant, the angular momentum of each blade must also remain constant

"bVi =

or

2 2

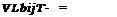Wi =

After dividing through by m, we obtain = COnst. We see from

this equation that during upward blade flapping (Г2<ґі) the angular velocity must increase or<ler that the angular momentum conservation law not /63

be violated. A force directed along the main rotor rotation is required in order to increase the angular velocity. This force will be the Coriolis or rotational force.

is defined as the product of the mass of the body

Fc = Vc

The Coriolis acceleration is found from the formula

jr = 2wV J C r

where is the relative or radial velocity of the blade center of gravity.

The velocity V (Figure 46a) can be defined as follows :

Vr = Vfl sin g.

Substituting the value of into the formula for the Coriolis acceleration, we obtain

Jc = 2wVfl sin 3.

The formula for the Coriolis force finally takes the form

Fc = 2 F wVfi sin 3’

Thus, the blade Coriolis force is directly proportional to blade weight, main rotor rpm, angular flapping velocity, and the flapping angle.

The Coriolis force for the advancing blade is directed in the direction of rotor rotation and increases as the blade approaches the 90° azimuth. Then it begins to diminish and becomes zero at the moment of equilibrium of the blade relative to the horizontal hinge.

The Coriolis force for the retreating blade will be directed aft, opposing rotor rotation, and reaches its maximal value at the 270° azimuth.

The blade Coriolis force develops the moment = F„r about the

Cor C c. g

main rotor axis (Figure 46b). For the main rotor with diameter D = 20 m without vertical hinges M^, ф 10,000 kgf’m.

Necessity for vertical hinges. We have established that the rotational drag and Coriolis forces act on the blades in the main rotor rotation plane.

At the 90° azimuth these forces are directed in opposite directions (see

Figure 46b). At the 270° azimuth these forces coincide in direction. While

the moment of the Coriolis force alone reaches a magnitude of about 10,000

kgf*m, the combined moment of the two forces (Coriolis and rotational drag)

will be considerably larger. This means that the blade root experiences large /64

loads in the rotor plane of rotation, which can cause rapid failure of the

blade if we consider that these loads alter their sign twice per revolution,

and the magnitude varies from the minimal to the maximal value twice per

revolution.

We encountered the loads created by the blade thrust moment previously.

These loads were eliminated with the aid of the horizontal hinge. In order to eliminate the bending moment in the hub rotation plane from the blade root, we must install a vertical hinge. When this hinge is used, the bending moment at the blade root will be zero, i. e., the blade will rotate forward (in the direction of rotor rotation) or aft about this hinge, performing oscillatory motions.