The Kutta-Joukowski Theorem and the Generation of Lift
Although the result given by Equation (3.140) was derived for a circular cylinder, it applies in general to cylindrical bodies of arbitrary cross section. For example,
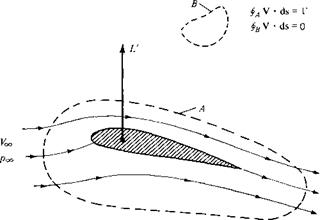
consider the incompressible flow over an airfoil section, as sketched in Figure 3.37. Let curve A be any curve in the flow enclosing the airfoil. If the airfoil is producing lift, the velocity field around the airfoil will be such that the line integral of velocity around A will be finite, that is, the circulation
![]() f> Vds
f> Vds
is finite. In turn, the lift per unit span L’ on the airfoil will be given by the Kutta – Joukowski theorem, as embodied in Equation (3.140):
 [3.140]
[3.140]
This result underscores the importance of the concept of circulation, defined in Section 2.13. The Kutta-Joukowski theorem states that lift per unit span on a two-dimensional body is directly proportional to the circulation around the body. Indeed, the concept of circulation is so important at this stage of our discussion that you should reread Section 2.13 before proceeding further.
The general derivation of Equation (3.140) for bodies of arbitrary cross section can be carried out using the method of complex variables. Such mathematics is beyond the scope of this book. (It can be shown that arbitrary functions of complex variables are general solutions of Laplace’s equation, which in turn governs incompressible potential flow. Hence, more advanced treatments of such flows utilize the mathematics of complex variables as an important tool. See Reference 9 for a particularly lucid treatment of inviscid, incompressible flow at a more advanced level.)
In Section 3.15, the lifting flow over a circular cylinder was synthesized by superimposing a uniform flow, a doublet, and a vortex. Recall that all three elementary flows are irrotational at all points, except for the vortex, which has infinite vorticity at the origin. Therefore, the lifting flow over a cylinder as shown in Figure 3.33 is
|
irrotational at every point except at the origin. If we take the circulation around any curve not enclosing the origin, we obtain from Equation (2.137) the result that Г = 0. It is only when we choose a curve that encloses the origin, where V x V is infinite, that Equation (2.137) yields a finite Г, equal to the strength of the vortex. The same can be said about the flow over the airfoil in Figure 3.37. As we show in Chapter 4, the flow outside the airfoil is irrotational, and the circulation around any closed curve not enclosing the airfoil (such as curve В in Figure 3.37) is consequently zero. On the other hand, we also show in Chapter 4 that the flow over an airfoil is synthesized by distributing vortices either on the surface or inside the airfoil. These vortices have the usual singularities in V x V, and therefore, if we choose a curve that encloses the airfoil (such as curve A in Figure 3.37), Equation (2.137) yields a finite value of Г, equal to the sum of the vortex strengths distributed on or inside the airfoil. The important point here is that, in the Kutta-Joukowski theorem, the value of Г used in Equation (3.140) must be evaluated around a closed curve that encloses the body, the curve can be otherwise arbitrary, but it must have the body inside it. r
At this stage, let us pause and assess our thoughts. The approach we have discussed above—the definition of circulation and the use of Equation (3.140) to obtain the lift—is the essence of the circulation theory of lift in aerodynamics. Its development at the turn of the twentieth century created a breakthrough in aerodynamics. However, let us keep things in perspective. The circulation theory of lift is an alternative way of thinking about the generation of lift on an aerodynamic body. Keep in mind that the true physical sources of aerodynamic force on a body are the pressure and shear stress distributions exerted on the surface of the body, as explained in Section 1.5. The Kutta-Joukowski theorem is simply an alternative way of expressing the consequences of the surface pressure distribution; it is a mathematical expression that is consistent with the special tools we have developed for the analysis of inviscid, incompressible flow. Indeed, recall that Equation (3.140) was derived in Section 3.15 by integrating the pressure distribution over the surface. Therefore, it is not quite proper to say that circulation “causes” lift. Rather, lift is “caused” by the net imbalance of the surface pressure distribution, and circulation is simply a defined quantity determined from the same pressures. The relation between the surface pressure distribution (which produces lift L’) and circulation is given by Equation (3.140), However, in the theory of incompressible, potential flow, it is generally much easier to determine the circulation around the body rather than calculate the detailed surface pressure distribution. Therein lies the power of the circulation theory of lift.
Consequently, the theoretical analysis of lift on two-dimensional bodies in incompressible, inviscid flow focuses on the calculation of the circulation about the body. Once Г is obtained, then the lift per unit span follows directly from the Kutta- Joukowski theorem. As a result, in subsequent sections we constantly address the question; How can we calculate the circulation for a given body in a given incompressible, inviscid flow?