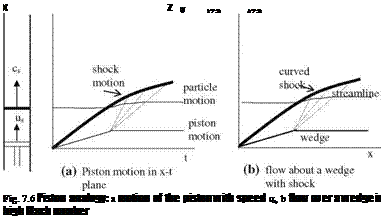
The Piston Analogy

Airfoils and control surfaces are thin and/or slender objects which cause free stream to make small angles with leading edge shocks and expansion waves when
the flow fields expand for Mach numbers grater than 4. For this reason, (1) the changes of speed in free stream directions are negligible compared to the speed changes in normal to free stream, and (2) similarly, the gradients of the flow parameters in the direction of the free stream are negligible compared to the gradients in normal direction. These two facts leads to following ‘in the unsteady flow around thin bodies a fluid column normal to the free stream moves in the flow direction while continuing its unsteady motion’. This fact was first observed by W. D. Hayes. Therefore, it is named ‘‘Hayes’ Hypersonic Analogy’’.

Using the Hayes’ Hypersonic Analogy, the pressure variation of two dimen­sional flows past an airfoil can be expressed in terms of the pressure change due to the waves created by unsteady motion of a piston in one dimensional cylinder (Lighthill 1953). Now, let us study in detail the approach given by Lighthill (Liepmann and Roshko).

According to the similarity law deduced from Fig. 7.6, the surface pressure ratio to the free stream pressure can be obtained using the concept of simple wave created by compression as follows (Liepmann and Roshko)

Here, w shows both the piston velocity and the vertical velocity at the wedge surface, and a indicates the sound of speed at the free stream. For Eq. 7.21 to be valid the flow must be isentropic which is possible only for the case of small perturbations. In addition, the vertical velocity w given by Eq. 7.21 is also valid for the unsteady flows. Let z = za (x, t) be the equation of the surface. The asso­ciated vertical velocity is then given by

Now, we can obtain the application areas of Eq. 7.21 to a profile with a thickness ratio of s with the free stream Mach number. Let в be the turning angle of the flow and w be the vertical velocity because of presence of the airfoil. The approximate value of the vertical velocity then becomes

w^Uh = aMh

This can be written as

w

ffi Mh (7.23)

The product Mh of Eq. 7.23 is called the hypersonic similarity parameter. The validity of the piston theory depends on this parameter. For piston theory to be valid, the hypersonic flow parameter must be very much less than 1. That is ‘the non dimensional turning speed in piston theory is restricted by the product of Mach number and the turning angle’.

Now, we can expand the right hand side of Eq. 7.21 into the series expressed in terms of w/a

Equation 7.24 is applicable for the hypersonic similarity parameter range 0 < Ms < 0.6. The lower order approximation can be made for 0 < Ms < 0.3 by neglecting the third term as

p w y(y + 1)

ffi 1 + c +

Pi a 4

Finally, the linear approach is valid for 0 < Ms < 0.15, and reads as

— ffi 1 + c w (7.26)

Pi a

Including the thickness effect of the airfoil gives better results for the piston theory when compared with the experimental results (Ashley and Zartarian 1956). At high Mach numbers the high flow speeds make the local density low. The low density, on the other hand lowers the value of the Reynolds number which in turn causes the boundary layer thickness to be high. This forces us to consider the profile thickness during the application of the piston theory on hypersonic flows. In addi­tion, in unsteady hypersonic flows there must also be restriction on the free stream Mach number M and the reduce frequency k as follows (Ashley and Zartarian 1956):

kM2 » 1 or (kM)2 » 1 (7.27)

The criterion given by Eq. 7.27 show that the piston theory is safely applicable at high reduced frequencies.

The piston theory introduced so far is applicable for Ms < 1 range. In real life, however, even for thin profiles we encounter some cases with Ms > 1, which will be examined in the next section.