The Pressure Drag of a Slender Body in Supersonic Flow

The pressure drag acting on a body in supersonic flow can be thought of as composed of two parts, the wave drag and the vortex drag (see further Chapter 9). If the body has a blunt base, there is, in addition, a base drag. The wave drag results from the momentum carried away by the pressure waves set up by the body as it travels at a speed greater than the speed of sound. In a subsonic flow there is, of course, no wave drag, since no stand­ing pressure waves are possible. The vortex drag arises from the momentum carried away by the vortices trailing from a lifting body and is governed by the same relations in both supersonic and subsonic flow.

The pressure drag of a slender body in a supersonic flow is most easily calculated by considering the flow of momentum through a control surface surrounding the body. We shall here follow essentially the approach taken by Ward (1949), which gives the total pressure drag but does not specify how the drag is split up into wave drag and vortex drag.

In Section 1-6 it was shown that, by considering the flow of momentum through a control surface S surrounding the body, the force on the body is given by

(1-51)

where n is the outward unit normal to the surface S, and Q is the velocity vector. It is convenient to introduce into (1-51) the perturbation velocity U„q = Q — it/*,, which gives

s

This may be simplified somewhat by use of the equation of continuity (cf. 1-45)

<£j>p(q + i) • n dS = 0. (6-68)

s

Hence, since S is a closed surface,

Fbody = —<0>l(p — Poo)n + pUlq(q « n + і * n)] dS, (6-69) s

which is the form we are going to use.

z 4 x

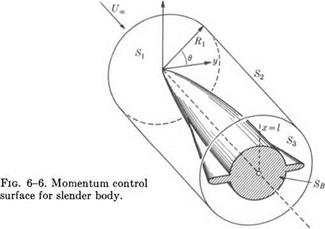
It is convenient in the present case to choose S in the manner shown in Fig. 6-6. Thus the surface S consists of three parts: Sx, S2, and S3, of which Si and S3 are circular disks and S2 a cylinder parallel to the main flow whose radius Rx will be chosen so that S2 is at the outer limit of the inner region. It is assumed that Sx lies ahead of the body so that the flow is undisturbed there, and S3 is located at the base section of the body. The body may have a blunt base, but the linearized theory is, of course, not valid for the calculation of the pressure on the base. We assume that the base pressure рв is known, so that the base drag contribution

Db = (p® — Pb)Sb (6-70)

to the total drag is given. In supersonic flow the effect of the blunt base will not be felt upstream of the base section. Hence the linearized theory may be used to calculate the flow ahead of the base section and thus the pressure drag on the remainder of the body.

Since S is located in the inner region, the flow is essentially incompres­sible so that, on S, p may be considered constant and equal to its free – stream value. The term q ■ n + і • n in (6-69) is simply the nondimensional velocity component normal to S. Thus, by taking the ж-component of (6-69) we obtain

Fig. 6-7. Drag rise at zero lift for a wing-body combination, for body alone, and for equivalent body. [Adapted from Whitcomb (1956). Courtesy of the National Aeronautics and Space Administration.]

PRESSURE DRAG, SLENDER BODY IN SUPERSONIC FLOW

This formula shows how the drag varies with Mach number. If S'(l) = 0, that is, if the body ends in a point or with a cylindrical portion, the drag becomes independent of the Mach number. Of particular interest is the drag of the equivalent body of revolution, for which

This is the equivalence rule for the pressure drag. It is a fairly easy matter to show that it must hold for all speed regimes whenever the equivalence rule for the flow is valid. Thus it will also hold for transonic speeds, and, as will be explained in Chapter 12, with less restrictions than for sub – or supersonic speeds.

In many cases the right-hand side of (6-87) is zero and hence the drag equal to that of the equivalent body of revolution. This occurs whenever:

(a) The body ends with an axisymmetric portion so that the two parts in (6-87) cancel.

(b) The body ends in a point.

(c) The body ends in a cylindrical portion parallel to the free stream so that dip/dn and S’ are zero.

Most practical slender missile or airplane configurations satisfy (a) or

(c) . For such a body one can thus experimentally test the validity of the equivalence rule simply by comparing the pressure drag with that of the equivalent body of revolution. Such measurements were made by Whitcomb (1956). Some of his results are reproduced in Fig. 6-7.

The agreement is good in the transonic region when the viscous drag has been separated out. From these results Whitcomb drew the conclusion that it should be possible to reduce the drag of a slender wing-body com­bination by indenting the body so that the equivalent body of revolution would have a smooth area distribution. This is the well-known transonic area rule, which has been used successfully to design low-drag configura­tions for transonic airplanes. The savings in drag that can be achieved are demonstrated in Fig. 6-7 (b).

6-7 Transverse Forces and Moments on a Slender Body

The transverse forces and moments (lift, side force, pitching moment, etc.) on a slender body can be obtained by considering the flow of mo­mentum through a control surface surrounding the body, as in the preced­ing section. However, we shall instead use a different method that makes use of results previously deduced for unsteady constant-density flow.

Let x, yi, Zi be a coordinate system fixed with the fluid so that

xi = x — UJ, yi = у, z = г. (6-88)

An observer in this coordinate system will see the body moving past with a velocity in the negative aq-direction. Consider now the fluid motion in a slab of width dxi perpendicular to the free stream as the body moves past. The crossflow in the neighborhood of the body will be governed by the equations for two-dimensional constant-density flow in the crossflow plane, but the flow will now be unsteady since consecutive cross sections of the body pass through the slab as the body travels by. The incompres­sible crossflow in the slab will thus be that around a two-dimensional body that changes shape and translates with time (and also rotates if rolling of the slender body is considered). This situation is illustrated in Fig. 6-8.

Since the flow has no circulation in the crossflow plane we can directly apply the methods developed in Section 2-4. [The Blasius’ equation (2-122) for unsteady flow is not applicable since it was derived under the assumption that the cross section does not change with time.] Thus, if £ is the crossflow momentum vector per unit body length, the force acting on the body cross section of width dx is, according to (2-61),

dF = jY + kL = – dxx ^ , (6-89)

where L is the lift and Y is the side force. The momentum vector £ is given by (2-54). Thus, in two-dimensional flow,

£ = —y>ia. ds,

where ipi is ip expressed in (x1: ylt zlt t) and the integral is to be taken around the (instantaneous) body cross section. The factor £/„ comes from the defini­tion of <p. It follows from Fig. 6-9 that

n ds = (j cos в + к sin в) ds

= j<fei — kdyi. (6-91)

Hence

£ = —f A^i(zi) dzi

— pxUJs. /Ду 1(2/1) dyu (6-92)

where Д<рі(уі) is the difference in <p between the upper and lower surfaces of the cross section and t<pi(zi) is the difference in <pi between the right and left surfaces of the cross section. Introducing (6-92) into (6-89) we thus obtain

By integrating over the body length, total lift, pitching moment, etc. can then be obtained. Particularly simple are the expressions for the total forces, which become

(6-97)

(6-98) where С в indicates that the integral is to be evaluated at the base cross

section. In order to calculate total forces, one thus only needs the cross flow at the base. Frequently, the flow is given in complex variables, in which case it is convenient to work with the complex force combination

X = у + iz.

[This formula could, of course, also have been obtained by introducing the complex vector directly in (6-92).] The idea is then to introduce the complex potential W(X) = <p + іф, which would reduce the problem to that of evaluating a closed-contour complex integral. However, a direct replacement of <p by W will generally lead to an incorrect result unless the stream function ф happens to be zero, or constant, along the cross section contour. We therefore introduce, as in (6-59), the potential W’ for the related flow having zero normal velocity at the contour and velocity components at infinity proportional to the side-slip angle and angle of attack, respectively, at the base section. Thus

<p = Re {W'(X)} – aBz – РвУ, (6-100)

where а в and fis are the angle of attack and side-slip angle at the base (which would be different, from the overall angle of attack and side slip if the body were cambered). Now ф’ is zero along the contour, and we may therefore set

F = —ip„UxWV?’ dX — iPxUxSb(oib — іРв), (6-101)

where Sb is the base area. The last term follows from simple geometrical considerations that give, for example, that

In the first integral of (6-101) we may choose any path of integration that encloses the base contour, the most convenient one being a large circle at infinity. Assuming that W’ may be expressed by the following Laurent series for large |X|

w’ = «0x+x;^f, (6-юз)

and a_! being the residue at infinity, we obtain from (6-101)

and inserting the residue as given by the second term of (6-105), the fol­lowing result is obtained

L = irpaUla(s2 – R2 + R*/s2)B, (6-106)

where index В refers to the base section. (The side force is, of course, zero in this case.) This result contains as special cases those of the wing alone and body alone. In the latter case, setting sB = Rb in (6-106) we obtain

L = wpooU2R2Ba, (6-107)

that is, the lift coefficient based on the base area is simply

CL = 2a,

a result first derived by Munk (1924). An interesting conclusion from this is that on a body pointed at the rear no lift is exerted, only a pitching

moment. This is destabilizing, tending to increase the angle of attack (cf. ellipsoid example in Chapter 2 and Fig. 2-5). In reality, viscous effects will cause a small positive lift.

For the case of a wing alone (Rb = 0), (6-106) gives

L = 7гроо U&s%oc. (6-109)

Hence, any slender wing with a straight, unswept trailing edge will have a lift coefficient (R. T. Jones, 1946)

CL = ?Aa. (6-110)

Comparisons for delta wings with experiments and a numerical lifting – surface theory, presented in Fig. 6-10, show that this simple formula overestimates the lift by 10% and more for A > 1.0.

It should be pointed out that (6-106) and (6-109) hold only for wings having monotonically increasing span from the pointed apex to the base section, otherwise sections forward of the base section will produce a wake that will influence the flow at the base, so that it no longer becomes inde­pendent of the flow in other cross sections. For the case of an uncambered wing with swept-forward trailing edges, one can easily show that the lift on sections behind that of the maximum span is zero in the slender – wing approximation, and hence (6-109) will hold if Sb is replaced by Smai, the maximum semispan. In the case of swept-back trailing edges, as for an arrowhead or swallowtail wing, Mangier (1955) has shown that the determination of the flow requires the solution of an integral equation.

A practically useful formula to estimate the effect of a fuselage on total lift is obtained by dividing (6-106) by (6-109). Thus

^™g±body = 1 _ (RbY + (RbY t (6_ln)

which shows that the body interference tends to decrease the lift.