Three-Dimensional Doublet
Consider a sink and source of equal but opposite strength located at points О and A, as sketched in Figure 6.2. The distance between the source and sink is l. Consider an arbitrary point P located a distance r from the sink and a distance rx from the source. From Equation (6.7), the velocity potential at P is
Let the source approach the sink as their strengths become infinite; that is, let
In the limit, as / —> 0, r — rx —> OB = l cosd, and rrx —»■ r2. Thus, in the limit, Equation (6.8) becomes
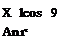 , X r-rx
, X r-rx
Ф = — hm————–
An rrx
![]()
|
|
||
|
where д = Л/. The flow field produced by Equation (6.9) is a three-dimensional doublet’ д is defined as the strength of the doublet. Compare Equation (6.9) with its twodimensional counterpart given in Equation (3.88). Note that the three-dimensional effects lead to an inverse r-squared variation and introduce a factor 47Г, versus 2тг for the two-dimensional case.
From Equations (2.18) and (6.9), we find
The streamlines of this velocity field are sketched in Figure 6.3. Shown are the streamlines in the zr plane; they are the same in all the zr planes (i. e., for all values of Ф). Hence, the flow induced by the three-dimensional doublet is a series of stream surfaces generated by revolving the streamlines in Figure 6.3 about the г axis. Compare these streamlines with the two-dimensional case illustrated in Figure 3.18; they are qualitatively similar but quantitatively different.
Note that the flow in Figure 6.3 is independent of Ф; indeed, Equation (6.10) clearly shows that the velocity field depends only on r and 9. Such a flow is defined as axisymmetric flow. Once again, we have a flow with two independent variables. For this reason, axisymmetric flow is sometimes labeled “two-dimensional” flow. However, it is quite different from the two-dimensional planar flows discussed earlier. In reality, axisymmetric flow is a degenerate three-dimensional flow, and it is somewhat misleading to refer to it as “two-dimensional.” Mathematically, it has only two independent variables, but it exhibits some of the same physical characteristics as general three-dimensional flows, such as the three-dimensional relieving effect to be discussed later.
![]()
|














