Three-Dimensional Source

Return to Laplace’s equation written in spherical coordinates, as (3.43). Consider the velocity potential given by	given by Equation
C ф =—— r	[6.1]
where C is a constant and r is the radial coordinate from the origin. Equation (6.1) satisfies Equation (3.43), and hence it describes a physically possible incompressible, irrotational three-dimensional flow. Combining Equation (6.1) with the definition of the gradient in spherical coordinates, Equation (2.18), we obtain
V = V0 = rL	[6.2]
In terms of the velocity components, we have
C V’ = ~ r1	[6.3a]
■ о II s?	[6.3b]
II О	[6.3c]

Clearly, Equation (6.2), or Equations (6.3a to c), describes a flow with straight stream­lines emanating from the origin, as sketched in Figure 6.1. Moreover, from Equation

(6.2) or (6.3a), the velocity varies inversely as the square of the distance from the origin. Such a flow is defined as a three-dimensional source. Sometimes it is called

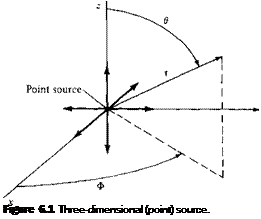simply a point source, in contrast to the two-dimensional line source discussed in Section 3.10.

To evaluate the constant C in Equation (6.3a), consider a sphere of radius r and surface S centered at the origin. From Equation (2.46), the mass flow across the surface of this sphere is

Hence, the volume flow, denoted by A., is

On the surface of the sphere, the velocity is a constant value equal to Vr = С/г2 and is normal to the surface. Hence, Equation (6.4) becomes

C 7

—г 4тсг2 = 4лС rz

TT A

Hence, C = —

47Г

Substituting Equation (6.5) into (6.3a), we find

Compare Equation (6.6) with its counterpart for a two-dimensional source given by Equation (3.62). Note that the three-dimensional effect is to cause an inverse r – squared variation and that the quantity 4л appears rather than 2л. Also, substituting

Equation (6.5) into (6.1), we obtain, for a point source,

In the above equations, X is defined as the strength of the source. When X is a negative quantity, we have a point sink.