Unexpected effects

Some of the practical implications of the relationships between speed and pres­sure are rather surprising at first sight. We might instinctively imagine that if air is squeezed through a converging duct, as illustrated in Fig. 1.10, the pres­sure would increase in the narrow part. At low speeds, this is not the case. If there are no leaks, then the same quantity of air per second must pass through the wide part as through the narrow part. Therefore, as the width of the duct decreases, the speed must increase. This increase in speed must be accompanied by a decrease in pressure. Thus, the pressure becomes lower as the duct nar­rows. We shall see later, however, that a different situation can occur when the flow speed approaches or exceeds the speed of sound.

Wing circulation

As we have stated, lift is produced as a consequence of the pressure difference between the upper and lower surfaces of the wing. This pressure difference is

related to the difference in the relative air speeds on the two surfaces, by the Bernoulli relationship given above. Hence, the amount of lift generated is related to the difference in relative speeds between upper and lower surfaces.

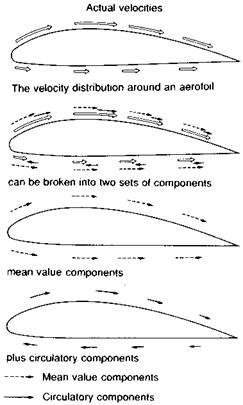
Referring to Fig. 1.11, we see that the speed of the air over any point on the upper surface can be considered as being a mean speed Vm plus a small com­ponent, whilst the speed of air flowing under the wing is Vm minus a small component.

From Fig. 1.11, we can see that the difference in the upper and lower surface air speeds is thus equivalent to adding, or superimposing, a rotational move­ment (indicated by the small black arrows) on to the average or mean motion at speed Vm (indicated by the dashed arrows).

Note that in this situation no individual particle of air actually travels around the profile in a complete circuit. The air flow may be thought of as merely having a circulatory tendency.

We measure the strength of the circulatory tendency by a quantity called the circulation; normally denoted by the letter K or the Greek letter Г. We will not concern ourselves here with an exact mathematical definition of circulation. In simple terms, increasing the circulation at a given flight speed, means increas­ing the difference in relative air flow speed between the upper and lower sur­faces, and hence, increasing the lift. The lift generated per metre of span is in fact equal to the product of the air density (p), the free-stream air speed (V), and the circulation (K).

L = pVK (per unit span).

Note that this means that the faster the flight speed (at a fixed altitude), the less will be the circulation required to generate a given amount of lift.