Uniform Flow: Our First Elementary Flow

In this section, we present the first of a series of elementary incompressible flows which later will be superimposed to synthesize more complex incompressible flows. For the remainder of this chapter and in Chapter 4, we deal with two-dimensional steady flows; three-dimensional steady flows are treated in Chapters 5 and 6.

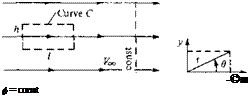
Consider a uniform flow with velocity V7^ oriented in the positive a direction, as sketched in Figure 3.19. It is easily shown (see Problem 3.8) that a uniform flow is a physically possible incompressible flow (i. e., it satisfies V • V = 0) and that it is irrotational (i. e., it satisfies V x V = 0). Hence, a velocity potential for uniform flow can be obtained such that Уф = V. Examining Figure 3.19, and recalling Equation

(2.156) , we have

3 ф r,

— = и = Voo [3.49a]

3a

3 ф

and — = u = 0 [3.49b]

dy

Integrating Equation (3.49a) with respect to a, we have

Ф — УЖХ + f(y) [3.50]

where f(y) is a function of у only. Integrating Equation (3.49b) with respect to y, we obtain

ф = const + g(x) [3.51]

where g(x) is a function of a only. In Equations (3.50) and (3.51), ф is the same function; hence, by comparing these equations, g(x) must be V~^ a, and /(>’) must be constant. Thus,

ф = VooA + const

Note that in a practical aerodynamic problem, the actual value of ф is not significant; rather, ф is always used to obtain the velocity by differentiation; that is, Уф = V. Since the derivative of a constant is zero, we can drop the constant from Equation (3.52) without any loss of rigor. Hence, Equation (3.52) can be written as

[3.53]

Figure 3.19 Uniform flow.

Equation (3.53) is the velocity potential for a uniform flow with velocity Vqo oriented in the positive x direction. Note that the derivation of Equation (3.53) does not depend on the assumption of incompressibility; it applies to any uniform flow, compressible or incompressible.

Consider the incompressible stream function 1js. From Figure 3.19 and Equations (2.150a and b), we have

	w v dy	[3.54 a]
and	dfi _ v__Q dx	[3.54b]

Integrating Equation (3.54a) with respect to у and Equation (3.54b) with respect to x, and comparing the results, wc obtain

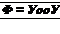[3.55]

Equation (3.55) is the stream function for an incompressible uniform flow oriented in the positive x direction.

From Section 2.14, the equation of a streamline is given by i/r = constant. Therefore, from Equation (3.55), the streamlines for the uniform flow are given by i/f = Vooy = constant. Because is itself constant, the streamlines are thus given mathematically as у = constant (i. e., as lines of constant y). This result is consistent with Figure 3.19, which shows the streamlines as horizontal lines (i. e., as lines of constant y). Also, note from Equation (3.53) that the equipotential lines are lines of constant*, as shown by the dashed line in Figure 3.19. Consistent with our discussion in Section 2.16, note that the lines of ijr = constant and ф = constant are mutually perpendicular.

Equations (3.53) and (3.55) can be expressed in terms of polar coordinates, where x = r cos 9 and у = r sin 9, as shown in Figure 3.19. Hence,

[3.56]

Consider the circulation in a uniform flow. The definition of circulation is given by

Г = – j> Vds [2.136]

Let the closed curve C in Equation (2.136) be the rectangle shown at the left of Figure 3.19; h and l are the lengths of the vertical and horizontal sides, respectively, of the rectangle. Then

V • ds = – Уооl – 0(h) + V^l + 0(h) = 0

or	Г = 0	[3.58]

Equation (3.58) is true for any arbitrary closed curve in the uniform flow. To show this, note that Voo is constant in both magnitude and direction, and hence

because the line integral of ds around a closed curve is identically zero. Therefore, from Equation (3.58), we state that circulation around any closed curve in a uniform flow is zero.

The above result is consistent with Equation (2.137), which states that

[2.137]

We stated earlier that a uniform flow is irrotational; that is, V x V = 0 everywhere. Hence, Equation (2.137) yields Г = 0.

Note that Equations (3.53) and (3.55) satisfy Laplace’s equation [see Equation

(3.41) ], which can be easily proved by simple substitution. Therefore, uniform flow is a viable elementary flow for use in building more complex flows.