Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Unsteady Potential Flow
The Helmholtz vorticity transport equation (1.95) dictates that aerodynamic flows have zero vorticity everywhere except in thin viscous layers adjacent to a solid body and in its trailing wakes. This conclusion remains valid for unsteady flows.
ш = Vx V = 0 (outside viscous layers) (7.5)
Furthermore, the low-speed continuity equation is unchanged in the unsteady case,
а = V – V = 0 (7.6)
so that the velocity field still has zero divergence everywhere in the flow interior. The overall conclusion is that the physical constraints on the vorticity and source distributions are the same in both steady and unsteady low speed flows. The instantaneous velocity field outside the viscous layers (or the entire Equivalent Inviscid Flow, introduced in Chapter 3) can still be represented by the perturbation potential P(r, t).
V(r, t) = Vp (7.7)
If source sheets and doublet sheets are used as in most panel methods, then the unsteady potential can be expressed explicitly via the usual superposition integrals, which now have unsteady sheet strength distributions.
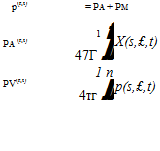
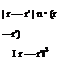(7.8)
(7.9)
(7.10)
