Variation of lift along the span

The theory of vortex behaviour that predicted a closed circuit also indicates that a steady vortex cannot vary in strength along its length. However, it was soon found that real wings do not generally produce the same amount of lift per metre of span at the centre as they do at the tips, so the horseshoe vortex system shown in Fig. 2.3 is clearly an over-simplification.

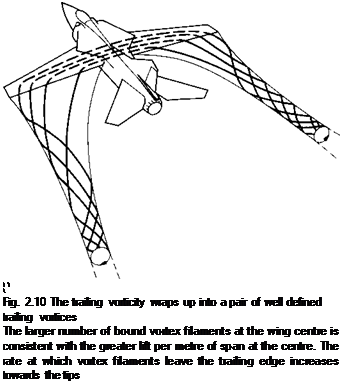The solution proposed by Lanchester, is to imagine a whole series of horse­shoe vortex lines or ‘filaments’, as shown in Fig. 2.10. At the centre of the wing,

where the lift per metre of span is greatest, there is the largest number of vortex lines. If you refer back to Fig. 2.6(b), you will see that just downstream of the wing trailing edge, there is a rotational tendency or vorticity across the whole of the span, even though it only forms a clearly defined vortex near the tips. By making horseshoe vortex shapes of different spans, we can represent the way that vorticity is shed all along the span. In Fig. 2.10, we show how this vorticity wraps up into a single pair of well defined trailing vortices.

The fact that the rotational tendency occurs all along the wing, just down­stream of the trailing edge, rather than only at the tips, ties up with the phys­ical behaviour shown in Fig. 2.6.

Figure 2.10 is similar to the diagram originally given by Lanchester in 1897. Unfortunately, his ideas were not immediately understood, and they were not published until 1907. Lanchester was not good at describing his work in clear language, and he had a habit of making it sound bogus by inventing pompous words such as phugoid (which we shall encounter later) and aerofoil!

The German engineer Ludwig Prandtl, who had been working along similar lines, developed these ideas into a usable mathematical model. The so-called Lanchester-Prandtl theory represented a major breakthrough in the under­standing of aircraft flight. It also forms the basis of mathematical theories in which the wing-bound and trailing vorticity are represented by a large array of vortex lines or rings. Although we are not concerned with mathematics in this book, the concepts involved in the Lanchester-Prandtl theory can be helpful to our appreciation of the physical principles of aircraft aerodynamics.