Vector, Dyadic, Matrix, and Tensor Forms
Bryan used quite conventional cartesian coordinates in the derivation of the equations of airplane motion on moving axes, in 1911. Cartesian coordinates were used as well by subsequent investigators, such as B. Melvill Jones (1934), Charles Zimmerman (1937), and Courtland Perkins (1949). The first author who applied vector methods to the derivation of these equations appears to have been Louis M. Milne-Thomson, in his book Theoretical Aerodynamics (1958).
The most notable thing about the Milne-Thomson vector derivation is the way in which a fundamental moving axis rate equation is developed. This is the relationship between vector
|
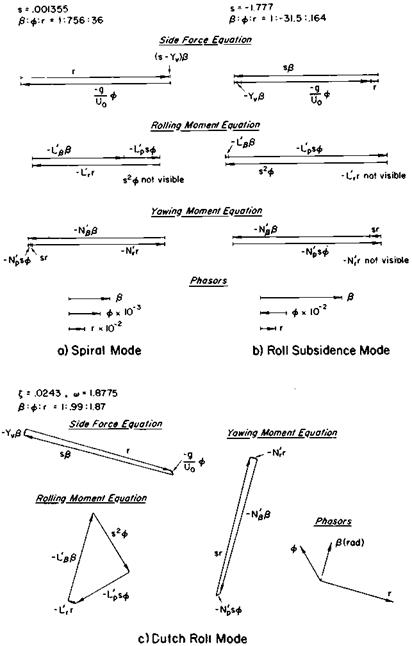
Figure 18.9 Time vector diagrams for a conventional airplane, from Aircraft Dynamics and Automatic Control by McRuer, Ashkenas, and Graham (1973). Sideslip angle в is almost nonexistent in the spiral mode. Bank angle Ф dominates in the roll subsidence mode. All motions are of the same order of magnitude in the Dutch roll mode. |
rates of change referred to inertial axes, required for application of Newton’s law of motion, and vector rates of change as seen on moving axes. A simple vector cross-product connects the two rates of change. Milne-Thomson’s vector equations of airplane motion on moving axes is of course far more compact than the cartesian form. In Theoretical Aerodynamics, Milne-Thomson did extend the vector derivation to the small-perturbation case.
Dyadics are generalized vectors, having nine instead of three components. Rigid-body moments of inertia and angular momenta have particularly simple dyadic forms. Dyadic versions of the torque or rotational equations of airplane motion are readily found, but there is no particular advantage to the dyadic form of the ordinary equations of motion. An advantage does occur for the semirigid case where the relative angular velocities of linked rigid bodies are computed (Abzug, 1980).
On the other hand, matrix forms of the equations of airplane motion on moving axes now have a significant role in flight dynamics. This is the result of the marvelous matrix manipulation capability of modern digital computers. The linearized equations of airplane motion are put into matrix form by first expressing the equations in state-variable form. In the state-variable formulation, a first-order differential equation is written for each degree of freedom of the system.
The matrix form is {x} = [A ] {x} + [B] [u }, where, for the airplane,
{x} is a N-by-1 state vector formed of the perturbation airplane motion states, such as u, v, and w.
{x} is the time derivative of {x}.
[A ] is a N-by-N system matrix formed of stability derivatives, such as dX/du, mass, and dimensional properties.
[B ] is an N-by-M control matrix formed of control derivatives such as дX/dS.
{u} is a M-by-1 control vector formed of perturbation control surface angles.
For the perturbation longitudinal equations a typical state vector {x} is the 5-by-1 vector {u а в q h}. A typical control vector {u} is the 1-by-1 vector, hence scalar, {Sh}, the stabilizer angle. For the perturbation lateral equations {x} is typically the 6-by-1 vector {в ф p ф ry}. The control vector is usually the 2-by-1 vector {Sa Sr}.
Modern matrix flight control analysis and synthesis methods generally augment the airplane state vector with control system states and manipulate matrices [A] and [B] in closed-loop operations. All of the classical Bryan, Gates, Zimmerman, and Perkins analyses for the unaugmented airframe can be carried out with standard computerized matrix manipulations. A prime example is the method of finding transient solutions by forming transition equations from one interval to the next. Transition matrices are computed using large numbers of successive matrix multiplications.
Matrix methods are fundamental to a number of commercially available flight dynamics computer programs. Systems Technology, Inc., of Hawthorne, California, offers the “Linear System Modeling Program,” which does every possible form of linearized stability analysis, including time-vector analysis. The Design, Analysis and Research Corporation of Lawrence, Kansas, produces the “Advanced Aircraft Analysis” program, which does stability and control preliminary design, trim, and flight dynamics. Large general-purpose matrix manipulation computer programs such as “MATLAB” from MathWorks and “Mathcad” from MatSoft are also commercially available to the stability and control engineer.
The remarks about the dyadic form of the equations of airplane motion apply as well to tensor forms. That is, there is no special advantage in expressing the ordinary equations of rigid-body airplane motion in tensors, as compared with cartesians or vectors. Zipfel (2000) uses a tensor form of the rigid-body equations of airplane motion on moving axes.