Vertical Climb
Helicopter flight along a vertical trajectory with constant velocity is
termed the vertical climb regime. The following forces act on a helicopter
in vertical climb (see Figure 53): the helicopter weight force G, the main
rotor thrust force T, and the tail rotor thrust force T.
t. r
In order to balance the tail rotor thrust force, the main rotor thrust force vector must be inclined at the angle 6, which results in the creation of the vertical thrust force component Y and the horizontal component S^.
The steady-state climb conditions will be expressed by the equalities:
Since the force X is small and may be neglected and the force YftS T, the equality Y = G + X can be replaced by the equality T = G. Then the vertical climb conditions will be analogous to the hovering conditions. The condition T = G assures constant helicopter speed in the vertical climb regime./82 The equality Tt r = Ss assures rectilinear flight.
Power required for vertical climb. The difference between the hovering
and vertical climb conditions is that, first, the force X in the vertical
par
climb is larger than in hovering, since it depends on two velocities: the
vertical velocity and the induced velocity V^.
Second, while in hovering the equality T = G assures a state of relative rest; in climb the same equality must assure constant velocity of the vertical motion.
Consequently, the work per unit time of the thrust force in a vertical climb is different from that in a hover; during climb this work is made up of the work expended on creating the thrust force equal to the weight (TV^ =
= GV^), and the work expended in creating the vertical velocity (TV ). During hovering, the work per unit time of the thrust force is expended only in creating the induced flow velocity and is equal to TV_^.
Therefore, while the induced power required for hover is found from the formula
the induced power required for vertical climb is expressed by the formula
For a low climb velocity (2-3 m/sec) the induced velocity differs very little
from the induced velocity in hovering, i. e., V. « V. . But this implies
that the induced power in a climb is greater than the hovering power by the magnitude AN (the excess power required for climb in comparison with the hovering power required). Bearing in mind that the profile power in climb is practically equal to the profile power in hover, we can express the formula for the power required for vertical climb through the hovering power formula
Vertical climb is possible only if excess power is available. To transition from hover to climb, the pilot increases the main rotor pitch with the aid of the "collective-throttle" lever; in this process the main rotor rpm remains nearly constant while the thrust increases. The helicopter transitions from hover to vertical climb. The thrust in a vertical climb can be determined from the formula of ideal rotor momentum theory T = 2pFV^V. In this case
+ V. As the vertical velocity increases the induced velocity will /83 decrease. Therefore, the main rotor thrust again decreases to the value the rotor had in hovering prior to increasing the collective pitch. Thus, in transitioning from hover to climb the pilot actually increases the power supplied to the rotor, but the main rotor thrust force remains nearly unchanged. Therefore,
![]() T, , but N = N, + AN. hov cl hov
T, , but N = N, + AN. hov cl hov
Vertical climb velocity. The vertical climb velocity is the height through which the helicopter center of gravity displaces in one second.
For vertical displacement of any body it is necessary to perform work equal to the product of the weight of the body by the height change, i. e.,
A = GH. Work performed per second is power. This means that to perform a climb additional power must be supplied to the main rotor, which is expended in creating the vertical velocity. This power is the excess power AN = GV^. Hence we find
(25)
The vertical velocity depends on the excess power and the helicopter weight. If the helicopter is heavily overloaded, there is sufficient engine
|
power only for hovering in the air cushion zone and in this case vertical climb is not possible.
The excess power used for vertical climb is equal to the difference between the power available and the power required for hover
Usually the helicopter excess power is not large and near sea level does not exceed 10-15% of the total engine power.
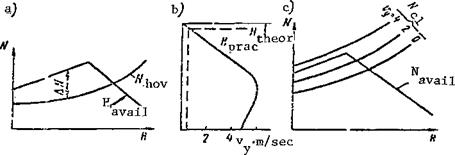
The vertical velocity at sea level amounts to 2-3 m/sec. The power available and engine power depend on the flight altitude, and with change of the altitude the vertical climb velocity will also change. The variation of the vertical climb velocity is determined by the altitude characteristics of the engine and is shown graphically (Figure 56a).
For a supercharged reciprocating engine the effective power will increase with increase of altitude from sea level to the critical altitude. The power required also increases. Therefore, the excess power may increase slightly or remain constant up to the critical altitude. After reaching the engine’s critical altitude the excess power decreases rapidly. Since the vertical velocity depends on the excess power, it will also decrease.
Using the graph of the variation of engine power and power required for /84 hovering as a function of altitude, we can use (25) to calculate V for various altitudes. On the basis of these calculations we can plot the vertical velocity as a function of altitude (Figure 56b), from which we see that the vertical velocity reaches its maximal value at the engine’s critical altitude, and then decreases.
The altitude at which the vertical climb velocity equals zero is called the helicopter’s static ceiling. The static ceiling is the highest altitude at which the helicopter can be hovered. At the static ceiling the excess power AN = 0.
However, since both AN and AV approach zero as the helicopter approaches the static ceiling, it is not possible to reach an altitude equal to the theoretical static ceiling. The "practical ceiling" concept has been introduced on this basis. The practical ceiling is the altitude at which the vertical climbing velocity equals 0.5 m/sec.
The static ceiling is defined in terms of rated engine power. A specific power required corresponds to each vertical velocity. Therefore, we can plot the power required for climb as a function of altitude for different vertical velocities (Figure 56c). From this graph we can find the vertical climb velocity at various altitudes for different power required. The altitude characteristic can be used to evaluate the possibility of climbing with a given vertical velocity.