Viscous Flow on Wedges

The pressure gradients that allow the Falkner-Skan equation to be an ordinary dif­ferential equation, given by:

1 1

Ux= cxm or p! = Pq – —p U2 = Po~2 p(cxm )2 (8.92)

correspond to the potential flow over wedges, as shown in Fig. 8.22.

u/U1 v/U i(Rex)1/2

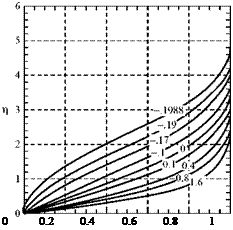
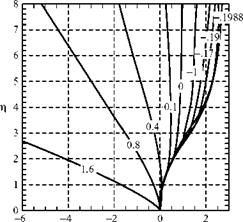
Figure 8.21. Solution of the Falkner-Skan equation for various values of the pressure-gradient parameter, p.

в	ЖР)	B(P)	f "(P,0)	П8(в)
-0.1988383	3.497798	0.868110	0.000000	5.0
-0.198800	2.332770	0.585389	0.005260	5.0
-0.190000	2.006747	0.576523	0.085702	4.7
-0.170000	1.778859	0.559664	0.162116	4.4
-0.140000	1.595897	0.538560	0.239737	4.2
-0.100000	1.442694	0.515044	0.319270	4.0
-0.050000	1.312361	0.490464	0.400323	3.9
0.000000	1.216779	0.469600	0.469600	3.7
0.100000	1.080320	0.435458	0.587035	3.5
0.200000	0.984159	0.408231	0.686708	3.4
0.300000	0.910995	0.385737	0.774755	3.2
0.400000	0.852636	0.366693	0.854422	3.1
0.500000	0.804550	0.350272	0.927681	3.0
0.600000	0.763974	0.335910	0.995837	2.9
0.800000	0.698683	0.311849	1.120269	2.8
1.000000	0.647904	0.292346	1.232589	2.6
1.200000	0.606902	0.276114	1.335723	2.5
1.400000	0.572872	0.262324	1.431587	2.4
1.600000	0.572872	0.262324	1.431587	2.3

Table 8.2. Properties of the numerical solutions for the Falkner-Skan equation

S(*) = hg (P),

, S * (x) = A(P)

There are several interesting special cases for various choices of the в value. For example, if m = 0 and в = 0, the Falkner-Skan equation collapses to the Blasius flat-plate equation. The factors of 2 that appear to be different between the two equations result from definitions of some of the parameters but do not change the outcome of the calculation.

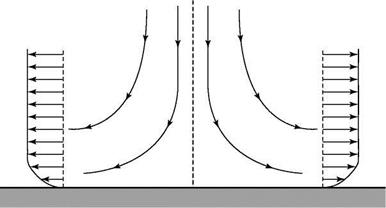
A useful special case is produced when m = 1 and в = 1. This yields the flow near a stagnation point, as illustrated in Fig. 8.23.

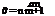
Figure 8.22. Wedge flow for the Falkner – Skan equation.

Figure 8.23. Flow near a stagnation point using the Falkner-Skan solution.

The external flow is expressed as:

U1 = u1x,

where for the case of the stagnation-point flow over a circular cylinder of radius R, the constant, Ui, is defined by:

9 U – щ = 2 -.

1 R

This is an important result because it can be helpful in starting numerical solutions in certain CFD applications, because the boundary-layer equations lose their validity near the stagnation point.