Consider a volume V in space. Let p be a scalar field in this space. The volume integral over the volume V of the quantity p is written as
 p dV = volume integral of a scalar p over the
p dV = volume integral of a scalar p over the
volume V (the result is a scalar)
|
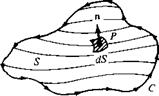
Figure 2.9 Sketch for surface integrals. The
three-dimensional surface area S is bounded by the closed curve C.
|
|
|
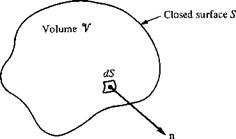
Figure 2.10 Volume V enclosed by the closed surface S.
|
|
|
Let A be a vector field in space. The volume integral over the volume V of the quantity A is written as
|
|
|
A dV = volume integral of a vector A over the volume V (the result is a vector)
|
|
|
2.2.11 Relations Between Line, Surface, and Volume Integrals
|
|
|
Consider again the open area S bounded by the closed curve C, as shown in Figure 2.9. Let A be a vector field. The line integral of A over C is related to the surface integral of A over S by Stokes ’ theorem:
|
|
|
|
|
Consider again the volume V enclosed by the closed surface S, as shown in Figure 2.10. The surface and volume integrals of the vector field A are related through the divergence theorem:
|
|
|
s
|
|
|
|
|
|
|
|
If p represents a scalar field, a vector relationship analogous to Equation (2.26) is given by the gradient theorem:
|
|
|
|
|
|
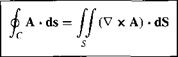
2.2.12 Summary
This section has provided a concise review of those elements of vector analysis which we will use as tools in our subsequent discussions. Make certain to review these tools until you feel comfortable with them, especially the relations in boxes.
![]() p dV = volume integral of a scalar p over the
p dV = volume integral of a scalar p over the![]()
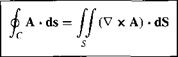
![]()













