Vortex Flow: Our Fourth Elementary Flow
Again, consulting our chapter road map in Figure 3.4, we have discussed three elementary flows—uniform flow, source flow, and doublet flow—and have superimposed these elementary flows to obtain the nonlifting flow over several body shapes, such as ovals and circular cylinders. In this section, we introduce our fourth, and last, elementary flow; vortex flow. In turn, in Sections 3.15 and 3.16, we see how the superposition of flows involving such vortices leads to cases with finite lift.
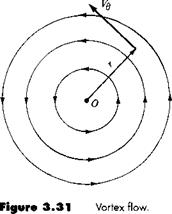
Consider a flow where all the streamlines are concentric circles about a given point, as sketched in Figure 3.31. Moreover, let the velocity along any given circular streamline be constant, but let it vary from one streamline to another inversely with distance from the common center. Such a flow is called a vortex flow. Examine Figure 3.31; the velocity components in the radial and tangential directions are Vr and Vg, respectively, where Vr = 0 and Vg = constant/r. It is easily shown (try it yourself) that (1) vortex flow is a physically possible incompressible flow, that is, V • V = 0 at every point, and (2) vortex flow is irrotational, that is, V x V = 0, at every point except the origin.
From the definition of vortex flow, we have
|
|
To evaluate the constant C, take the circulation around a given circular streamline of radius r
Comparing Equations (3.104) and (3.105), we see that
Г
C =———- [3.106]
2jr
Therefore, for vortex flow, Equation (3.106) demonstrates that the circulation taken about all streamlines is the same value, namely, Г = —2л C. By convention, Г is called the strength of the vortex flow, and Equation (3.105) gives the velocity field for a vortex flow of strength Г. Note from Equation (3.105) that Vg is negative when Г is positive; that is, a vortex of positive strength rotates in the clockwise direction. (This is a consequence of our sign convention on circulation defined in Section 2.13, namely, positive circulation is clockwise.)
We stated earlier that vortex flow is irrotational except at the origin. What happens at r = 0? What is the value of V x V at r = 0? To answer these questions, recall Equation (2.137) relating circulation to vorticity:
Г = ~jj(v x V)- dS [2.137]
Combining Equations (3.106) and (2.137), we obtain
![]() 2л C = j j (V x V) • dS
2л C = j j (V x V) • dS
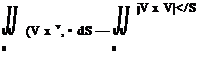 |
||
Since we are dealing with two-dimensional flow, the flow sketched in Figure 3.31 takes place in the plane of the paper. Hence, in Equation (3.107), both V x V and dS are in the same direction, both perpendicular to the plane of the flow. Thus, Equation (3.107) can be written as
In Equation (3.108), the surface integral is taken over the circular area inside the streamline along which the circulation Г = —2ттС is evaluated. However, Г is the same for all the circulation streamlines. In particular, choose a circle as close to the origin as we wish (i. e., let r —»■ 0). The circulation will still remain Г = —2лС. However, the area inside this small circle around the origin will become infinitesimally small, and
JJV x\dS ^ V x\dS [3.109]
s
Combining Equations (3.108) and (3.109), in the limit as r —>■ 0, we have
2тсС = |V x V| dS
2 тсС r,
or |VxV| = ——- [3.110]
dS
However, as r —>■ 0, dS —»■ 0. Therefore, in the limit as r —»■ 0, from Equation (3.110), we have
![]() |V x V|
|V x V|
Conclusion: Vortex flow is irrotational everywhere except at the point r = 0. where the vorticity is infinite. Therefore, the origin, r = 0, is a singular point in the flow field. We see that, along with sources, sinks, and doublets, the vortex flow contains a singularity. Hence, we can interpret the singularity itself, that is, point О in Figure
3.31, to be a point vortex which induces about it the circular vortex flow shown in Figure 3.31.
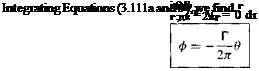 |
![Vortex Flow: Our Fourth Elementary Flow Подпись: [3.111a] [3.111Ы [3.1 12]](/img/3128/image574.gif) |
The velocity potential for vortex flow can be obtained as follows:
Equation (3.112) is the velocity potential for vortex flow.
 |
1 Зф
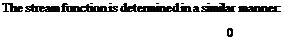
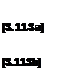 —- — = Vr
—- — = Vr
г Зв
Зф Г
dr в 2лг
Integrating Equations (3.113а and b), we have
Equation (3.114) is the stream function for vortex flow. Note that since ф = constant is the equation of the streamline, Equation (3.114) states that the streamlines of vortex flow are given by r = constant (i. e., the streamlines are circles). Thus, Equation
(3.114) is consistent with our definition of vortex flow. Also, note from Equation (3.112) that equipotential lines are given by в = constant, that is, straight radial lines from the origin. Once again, we see that equipotential lines and streamlines are mutually perpendicular.
At this stage, we summarize the pertinent results for our four elementary flows in Table 3.1.











