Vortex lift models

Polhamus [51] has developed a method for estimating vortex lift based on the leading-edge suction concept. In this formulation the leading edge suction force magnitude is obtained from the slender-body flow solution for a flate plate, corresponding to the geometry in Figure 6.12 with R = 0. This force is then applied normal to the surface rather than tangential to the surface, which in effect rotates it by 90° about the leading edge line. The equivalent formulation for general lifting surface geometries uses the leading edge suction force defined by equation (6.23), but applied in the normal direction.

/ "П 2

FSle = — pC n (at sharp leading edge) (6.80)

This rotation of the leading edge suction force from t to n models the boundary layer vorticity lifting off the surface and forming a free vortex sheet above the surface, as sketched in Figure 6.13 on the bottom right. The force rotation clearly increases the lift, and thus captures the vortex lift contribution. The lift increase reported by Polhamus matches experimental data fairly well.

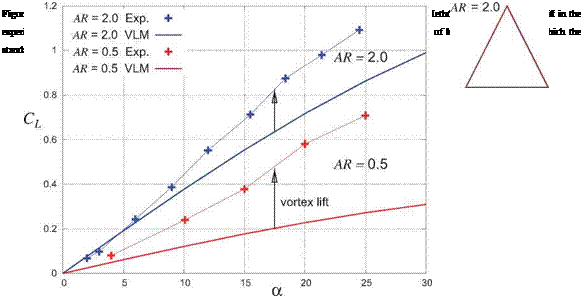The rotation of the leading edge suction force changes its direction from partly forward to partly aft, which significantly increases the drag. This effect on drag was also examined by Polhamus [52], with the conclu­sion that the added drag behaves much like induced drag from the added lift.