When Is A Flow Compressible?

As a corollary to Section 8.4, we are now in a position to examine the question, When does a flow have to be considered compressible, that is, when do we have to use analyses based on Chapters 7 to 14 rather than the incompressible techniques discussed in Chapters 3 to 6? There is no specific answer to this question; for subsonic flows, it is a matter of the degree of accuracy desired whether we treat p as a constant or as a variable, whereas for supersonic flow the qualitative aspects of the flow are so different that the density must be treated as variable. We have stated several times in the preceding chapters the rule of thumb that a flow can be reasonably assumed to be incompressible when M < 0.3, whereas it should be considered compressible when M > 0.3. There is nothing magic about the value 0.3, but it is a convenient dividing line. We are now in a position to add substance to this rule of thumb.

Consider a fluid element initially at rest, say, an element of the air around you. The density of this gas at rest is po. Let us now accelerate this fluid element isentropically to some velocity V and Mach number M, say, by expanding the air through a nozzle. As the velocity of the fluid element increases, the other flow properties will change according to the basic governing equations derived in Chapter 7 and in this chapter. In particular, the density p of the fluid element will change according to Equation

(8.43) ;

[8.43]

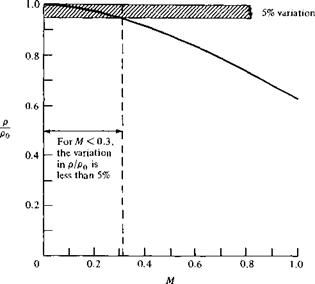
For у = 1.4, this variation is illustrated in Figure 8.6, where p/po is plotted as a function of M from zero to sonic flow. Note that at low subsonic Mach numbers, the variation of p/po is relatively flat. Indeed, for M < 0.32, the value of p deviates from po by less than 5 percent, and for all practical purposes the flow can be treated as incompressible. However, for M > 0.32, the variation in p is larger than 5 percent, and its change becomes even more pronounced as M increases. As a result, many aerodynamicists have adopted the rule of thumb that the density variation should be accounted for at Mach numbers above 0.3; that is, the flow should be treated as compressible. Of course, keep in mind that all flows, even at the lowest Mach numbers, are, strictly speaking, compressible. Incompressible flow is really a myth. However, as shown in Figure 8.6, the assumption of incompressible flow is very reasonable at low Mach numbers. For this reason, the analyses in Chapters 3 to 6 and the vast bulk of existing literature for incompressible flow are quite practical for many aerodynamic applications.

To obtain additional insight into the significance of Figure 8.6, let us ask how the ratio p/po affects the change in pressure associated with a given change in velocity. The differential relation between pressure and velocity for a compressible flow is given by Euler’s equation, Equation (3.12) repeated below:

Figure 8.6 Isentropic variation of density with Mach number.

This can be written as

ІЕ. = py2dV

P P V

This equation gives the fractional change in pressure for a given fractional change in velocity for a compressible flow with local density p. If we now assume that the density is constant, say, equal to po as denoted in Figure 8.6, then Equation (3.12) yields

{djA = P0y2dV V P Jo p y

where the subscript zero implies the assumption of constant density. Dividing the last two equations, and assuming the same dV/V and p, we have

dp/p = P_

(dp/p) о po

Hence, the degree by which p/po deviates from unity as shown in Figure 8.6 is re­lated to the same degree by which the fractional pressure change for a given dV/V is predicted. For example, if p/po = 0.95, which occurs at about M = 0.3 in Figure 8.5, then the fractional change in pressure for a compressible flow with local density p as compared to that for an incompressible flow with density p0 will be about 5 percent different. Keep in mind that the above comparison is for the local fractional

change in pressure, the actual integrated pressure change is less sensitive. For ex­ample, consider the flow of air through a nozzle starting in the reservoir at nearly zero velocity and standard sea level values of po = 2116 lb/ft2 and T0 = 510°R, and expanding to a velocity of 350 ft/s at the nozzle exit. The pressure at the nozzle exit will be calculated assuming first incompressible flow and then compressible flow.

Incompressible flow: From Bernoulli’s equation,

Vі T = To – — 2cn

Compressible flow: From the energy equation, Equation (8.30), with cp = 6006[(ft) (lb)/slug°R] for air,

From Equation (7.32),

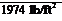p = 0.9329po = 0.9329(2116)

Note that the two results are almost the same, with the compressible value of pressure only 0.2 percent higher than the incompressible value. Clearly, the assumption of incompressible flow (hence, the use of Bernoulli’s equation) is certainly justified in this case. Also, note that the Mach number at the exit is 0.317 (work this out for yourself). Hence, we have shown that for a flow wherein the Mach number ranges from zero to about 0.3, Bernoulli’s equation yields a reasonably accurate value for the pressure—another justification for the statement that flows wherein M < 0.3 are essentially incompressible flows. On the other hand, if this flow were to continue to expand to a velocity of 900 ft/s, a repeat of the above calculation yields the following results for the static pressure at the end of the expansion:

Incompressible (Bernoulli’s equation): p = 1153 lb/ft2

Compressible: p = 1300 lb/ft2

Here, the difference between the two sets of results is considerable—a 13 percent difference. In this case, the Mach number at the end of the expansion is 0.86. Clearly, for such values of Mach number, the flow must be treated as compressible.

In summary, although it may be somewhat conservative, this author suggests on the strength of all the above information, including Figure 8.6, that flows wherein the local Mach number exceeds 0.3 should be treated as compressible. Moreover, when M < 0.3, the assumption of incompressible flow is quite justified.

M < 1 (subsonic flow)

M = 1 (sonic flow)

M > 1 (supersonic flow)

In the definition of M, a is the local speed of sound, a = л/yRT. In the theory of supersonic flow, it is sometimes convenient to introduce a “characteristic” Mach number M* defined as

и

a* where a* is the value of the speed of sound at sonic conditions, not the actual local value. This is the same a* introduced at the end of Section 7.5 and used in Equation (8.35). The value of a* is given by a* = *JyRT*. Let us now obtain a relation between the actual Mach number M and this defined characteristic Mach number M*. Dividing Equation (8.35) by u2, we have

(a/u)2 1 _ у + 1 / a*2

у – 1 2 “ 2(y – 1) V и )

(1/M)2 = y + 1 /J_2 _ 1

у – 1 2(y – 1) M*/ 2

2 2

M2 = —————— Z————-

(у + 1 )/M*2 – (у – 1)

Equation (8.47) gives M as a function of M*. Solving Equation (8.47) for M*2, we have

which gives M* as a function of M. As can be shown by inserting numbers into Equation (8.48) (try some yourself),

M* = 1	if M = 1
M* < 1	if M < 1
M* > 1	if M > 1
Iy + 1
M* It———— r	if M —>■ oo

у – 1

Therefore, M* acts qualitatively in the same fashion as M except that M* approaches a finite value when the actual Mach number approaches infinity.

In summary, a number of equations have been derived in this section, all of which stem in one fashion or another from the basic energy equation for steady, inviscid, adiabatic flow. Make certain that you understand these equations and become very

familiar with them before progressing further. These equations are pivotal in the analysis of shock waves and in the study of compressible flow in general.

Hence, M* = VA26 = 2.06, as obtained above.

In Example 3.1, we illustrated for an incompressible flow, the calculation of the velocity at a point on an airfoil when we were given the pressure at that point and the freestream velocity and pressure. (It would be useful to review Example 3.1 before going further.) The solution involved the use of Bernoulli’s equation. Let us now examine the compressible flow analog of Example 3.1. Consider an airfoil in a freestream where M^ — 0.6 and poo = 1 atm, as sketched in Figure 8.5. At point 1 on the airfoil the pressure is p = 0.7545 atm. Calculate the local Mach number at point 1. Assume isentropic flow over the airfoil.

Solution

We cannot use Bernoulli’s equation because the freestream Mach number is high enough that the flow should be treated as compressible. The free stream total pressure for Mx = 0.6 is, from Appendix A

Po. oo = — Poo = (1.276) (1) = 1.276 atm

Poo

pі = 0.7545 atm M, = ?

M = 0.6

Poo = 1 atm

This is the local Mach number at point 1 on the airfoil in Figure 8.5.

Note that flow velocity did not enter the calculations in Example 8.2. For compressible flow, Mach number is a more fundamental variable than velocity; we will see this time-and-time again in the subsequent sections and chapters dealing with compressible flow. However, we can certainly calculate velocities for compressible flow problems, but in such cases we usually need to know something about the temperature level of the flow. For the conditions that prevail in Example 8.2, calculate the velocity at point 1 on the airfoil when the free stream temperature is 59°F.

Solution

We will need to deal with consistent units. Since 0°F is the same as 460°R,

Too = 460 + 59 = 519°R

The flow is isentropic, hence, from Equation (7.32)

From Equation (8.25), the speed of sound at point 1 is

ai = JyRTi = У(1.4)(1716)(478.9) = 1072.6 ft/s

Hence,	V, = Midi = (0.9) (1072.6) =	965.4 ft/s