2-D Inviscid, Linearized, Thin Airfoil Theories

15.9.1.1 Incompressible Flow (M0 = 0)

Aerodynamic Center

The aerodynamic center is the point about which the moment of the aerodynamic forces is independent of the incidence a.

The aerodynamic center is located at the quarter-chord for all thin airfoils at low speeds.

Second Mode only Airfoil

Consider a thin cambered plate such that the vorticity distribution is given by the second mode with A2 > 0 as

Г'[x(t)]=2^{Ao1+nft + A 2 cos2t}
x (t) = 2 (1 – cos t), 0 < t < n

As seen in class

TO

d’[x (t)] = a – A0 + ^ An cos nt = a – A0 + A2 cos 2t

n=1

Integrating in t yields (using d (0) = d (c) = 0)

c

d (c) = (a – A0 + A2cos2t) sin t dt

02

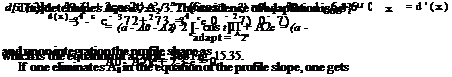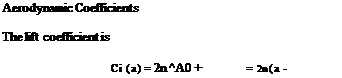= 2 J (a – A0 + A2(2 cos21 – 1)^ sin t dt

The moment coefficient

C„.0iO = – (A0 + A1 — f) = — (<> – 5^2)

The moment coefficient, at the aerodynamic center, is

7Г 7Г

Cm, a.c. = —4 (A1 — A2) = 4 A2

The drag coefficient is Cd — 0.

Moment About an Axis

The aerodynamic moment about the mid-chord is calculated, using the change of moment formula

1 n A2

Cm, c/2 = Cm, o (a) + 2 Cl(a) = 2 a +————- 6

If the profile is allowed to rotate without friction about an axis located at mid­chord, the equilibrium incidence, aeq, corresponds to Cmc/2 — 0, i. e.

aeq —

No, the equilibrium is unstable because dCmc/2/da — n/2 > 0.

15.9.1.2 Supersonic Flow (M0 > 1, в = yjM^ — 1)

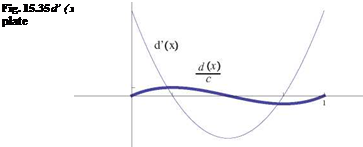
Consider the cubic plate of equation

4 x x x

d (x) = Ac 1 – 2 1 – , A > 0

3 c c c

The slope is given by

,4 x x2

d (x) = A 1 — 6 + 62 3 c c2

This plate equips the fins of a supersonic rocket.

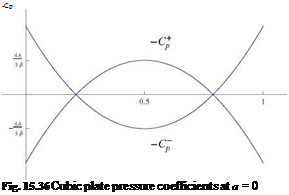
Pressure Distribution and Flow Features

At a = 0 the — C + and — C— are

, 2 , 8 x x2

—C + = — d'(x) = — A 1 — 6 + 6 2

— Cp = — d (x) = A 1 — 6 + 6

в

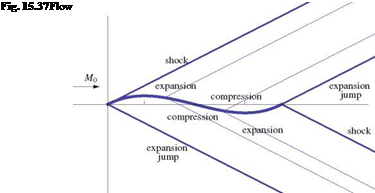
See Fig. 15.36.

The flow features (shocks, characteristic lines, expansion shocks are shown in Fig. 15.37).

Moment Coefficient

The moment coefficient (Cm,0) 0

, , 4 c. x dx 16 A 1 2

Cm-)a=0 = jl d (x>77 = -3×1 0 – « + K2) – d(

16 A -2 3 -4 n1

= – – 2-3 + 3 –

3в 2 2 .

For arbitrary a the moment coefficient reads

aa

Cm, o(a) = (Cm,0)a=0 — 2в = —в

Using the change of moment formula, the mid-chord moment can be evaluated as

1 a 1 a

Cm, c/2 = Cm, o(a) + Cl(a) = — 2 + 4 = 0

2 в 2 в

The moment is independent of a. This is expected, because the mid-chord is the aerodynamic center of thin airfoils in supersonic flow. The value is zero because it is the same as (Cm,0) 0.

There is equilibrium at any value of a. The equilibrium is neutral.