Active Treatments to Reduce Sound Radiation

In parallel to passive treatments, active control systems can also be added to shell structures in order to reduce their vibration and sound radiation (Maury et al. 2001; Maury et al. 2002c). The fundamental principles of active noise control dates back to the 1930’ (Gardonio 2010), however it took more than 50 years before the first applications were developed. This was due to both intrinsic limitations in the speed of the electronics for the controllers and to the limited technologies available for the sensor and actuator transducers. Nevertheless, the progress in digital electronics occurred in the second half of the twentieth century has brought to the development of fast processors with high computing power that enables the implementation of multi-channel controllers, which can manage the small time delays allowed for the implementation of noise and vibration control algorithms. In parallel, new types of transducers were developed, which have brought to the conception of new control systems. For example arrays of small size piezoelectric patch actuators or thin piezoelectric films were embedded in thin plates or shells to form composite structures with active layers (Bianchi et al. 2004; Aoki et al. 2008; Gardonio et al. 2010; Gardonio 2012). Alternatively electromechanical or magnetostrictive transducers were used to build small size proof-mass actuators that can be attached to thin structures to produce localised active effects (Preumont 2002; Preumont 2006; Gonzalez Diaz et al. 2008a; Gonzalez Diaz et al. 2008b; Gardonio and Alujevic 2010; Alujevic et al. 2011; Rohlfing et al. 2011). Such “smart structures” can be effectively used for the implementation of the so called “Active Structural Acoustic Control” (ASAC) systems for the reduction of the sound radiation by thin structures (Fuller et al. 1996; Gardonio and Elliott 2004; Gardonio and Elliott 2005b; Gardonio 2012).

In this section the basic principles of ASAC control are reviewed and then two examples of ASAC smart panels are described in more details with reference to the control of vibration and sound radiation due to a TBL excitation pressure field. Section 2 has shown that sound radiation is a rather complex phenomenon, which depends on the self and mutual radiation efficiencies between pair of modes of the structure. The fact that, as shown in Figure 8, at certain frequency bands the mutual radiation efficiencies may assume negative values indicates that the interaction between the vibration of pair of modes may lead to a “natural” reduction of the total radiation of noise. Thus, it is not so clear-cut that reducing the response of clusters of structural modes, for example of low order modes, leads to the control of the sound radiation at low frequencies. On the contrary it may bring to an increment of the sound radiation at some narrow frequency bands since the natural reduction of sound radiation between certain pairs of modes has been prevented. Several authors have studied the implementation of specific vibration control approaches aimed at the reduction of the sound radiation by structures. In this chapter the formulation proposed by Elliott and Johnson (1993) for the description of the sound radiation in terms of a new set of modes of the structure, which radiates sound independently, is considered. This is a simple and elegant formulation which directly leads to the conception of a new control paradigm where the sound radiation is reduced by controlling the vibration field of the most efficient radiation mode(s) of the structure. The formulation is based on the fact that the matrix a (®) with the self and mutual radiation efficiencies defined in Eq. (65) is normal, i. e. it is real, symmetric and positive definite. Thus the following eigenvalue-eigenvector decomposition can be implemented,

A»=P(®)rfi(®)P(®) , (85)

where p(®) is the [r x m ] orthogonal matrix of eigenvectors and a(®) is the [r x r ] diagonal matrix with real and positive eigenvalues. Therefore, the expression for the radiated sound power PSD in Eq. (64) can be rewritten as follows

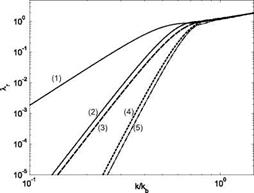
Figure 15. First five radiation efficiencies of the radition modes derived from the eigenvalue-eigenvector problem in Eq. (85).

SPr = 1 ®2Tr[П(®)Saa (®)] , (86)

where Saa (®) is the matrix of PSDs of the transformed complex modal responses а(®) that radiate sound independently from each other

a(ffl) = P (ffl)b (®) . (87)

Thus, considering Eq. (66), the matrix of the new modal responses Saa(a) is given by

Saa(®) – P(®)Y(®)Spp(®)Y"(w)P(w) . (88)

According to Eq. (85), the diagonal matrix with the eigenvalues П(«) provides the self radiation efficiencies of the new set of vibration modes, whose shapes can be reconstructed by linearly combining the natural modes of the panel with the eigenvectors. Thus the j-th radiation mode is given by

¥j (x, У, а) = ф(*, y)PT (®) (89)

where P,(®) is the j-th row of the matrix P(®). This expression indicates that the

radiation modes are frequency dependent. The plot in Figure 15 shows the first six eigenvalues, that is the first six radiation efficiencies, with reference to the ratio between the acoustic and flexural wave numbers k/kb in logarithmic scale.

(2,1)

(1,2)

(3,1)

(2,2)

The graph shows that, similarly to the self radiation efficiencies of the structural modes, the radiation modes are also characterised by rather small radiation efficiencies at low frequencies, which however rise rapidly with frequency up to the critical frequency where к = kb. At higher frequencies the radiation rises

further but at a lower rate. At low frequencies the radiation efficiency of the second and higher order radiation modes is much lower than that of the first radiation mode. Thus it is expected that controlling the vibration field related to

Figure 17. Sound radiation induced by TBL pressure field on smart panels
composed of: (a) a 3×3 array of decentralised velocity feedback loops using
idealised point velocity and point force sensor-actuator pairs and (b) a single
velocity feedback using an idealised distributed volume velocity sensor and an
idealised distributed uniform force actuator pair.

the first radiation mode should lead to a consistent reduction in the sound
radiation particularly at low frequencies below the critical frequency where
к = kb. The graphs in Figure 16 show the first five structural modes (column a)

and then the first five radiation modes at 100 and 800 Hz (respectively columns b and c) for the panel considered in this study. The first and most efficient radiation mode is therefore characterised by a volumetric shape, which tends to be rounded off along the borders as the frequency rises. This leads to the conclusion that, in order to control the vibration field of the panel associated to the first radiation mode, and thus to control the low frequency sound radiation, it is necessary to reduce the volumetric vibration of the panel. This may be achieved with an active system, which uses a distributed actuator that exerts a uniform force over the panel surface in such a way as to minimise an error signal provided by a sensor that measures the volumetric vibration of the panel. In principle, a multiple channel controller can be used, which simultaneously controls two or more radiation modes. However, this would be a rather complex system that marginally increments the control effects at low frequencies. In general, the active control of sound and vibration is based on two control architectures. When the primary disturbance to be controlled can be detected in advance, a feed-forward control architecture is implemented, which drives the control actuators in such a way as to produce a secondary acoustic or vibration field that destructively interferes with the primary disturbance field (Gardonio 2012). Alternatively, when the primary disturbance cannot be detected in advance, a feedback control architecture is used, which tends to modify the dynamic response of the system in such a way as to reduce the effect of the
primary disturbance (Gardonio 2012). Since the pressure field generated by TBL excitations is stochastic (both in time and in space domains) it is rather difficult to collect the reference signals that would allow the implementation of feed­forward control systems. Thus, feedback control systems are normally implemented to contrast the effects produced by TBL disturbances. In this chapter the two smart panels with the feedback systems shown in Figure 17 will be considered. System (a) comprises a 3x 3 array of decentralised feedback loops composed of an idealised force actuator with a collocated velocity sensor. The second system consists of a distributed uniform force actuator with a matched volume velocity sensor that implements a single absolute velocity feedback loop. In this case the feedback loop is aimed at controlling the volumetric vibration field of the panel, which, as discussed above, is the major contributor to sound radiation. The control of both feedback loops is proportional to velocity, thus it produces a damping effect. For this reason, these control systems are often reported as “active damping systems”. When the feedback loop or loops are implemented, the structural modal admittance matrix Y used to derive the kinetic energy PSD and radiated sound power PSDs is derived from the following modified version of Eq. (70)

[-аз2M + K(1 + Jrj) + JaDbr = fr, (90)

thus Y = [- a2M + K(1 + j^) + J«d] 1. The elements of the “active damping matrix” D for the system with the 3x 3 array of feedback loops are given by

Dpq =Z (X aMq (X s, ) , (91)

г-1

where g s is the gain implemented in the feedback loops and the vectors X a, i and Xs, i identify the positions of the i-th control actuator and i-th error sensor, which

are collocated in the specific case under consideration. The elements of the “active damping matrix” D for the system with the distributed uniform force actuator and distributed volume velocity sensor are instead given by

Dpq = gs Фр (xs)dSb JS фч (xs)dSb. (92)

where gs is the gain implemented in the feedback loop. In summary the total kinetic energy PSD and total radiated sound power PSD for the smart panels with arrays of point feedback loops or with a single feedback loop using distributed transducers have been derived from Eqs. (55) and (64) with the matrix of modal response PSDs S bbO) derived with Eq. (66) using the

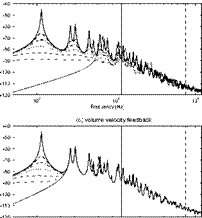Figure 18. PSD of the total kinetic energy (left-hand side plots) and total radiated sound power (right-hand side plots) per unit TBL pressure field PSD. Thick solid lines reference panel. Broken and solid-faint lines in plots (a, b) reference panel with 3×3 array of point velocity feedback loops with increasing feedback gains up to the optimal value that minimises the radiated sound power. Broken and solid-faint lines in plots (c, d) reference panel with the volume velocity-uniform force feedback loop with increasing feedback gains.

following expression for the matrix of modal addmittances У(ю) = [- су2 M + K (1 + jq) + jaDt]1.

Plots (a) and (b) in Figure 18 show the spectra of the total kinetic energy PSD and total radiated sound power PSD as the control gains of the 3×3 array of velocity feedback loops are increased. The broken and solid-faint lines in the two plots indicates that, as the feedback control gains are increased, the active damping action exerted by the feedback loops smoothens the resonance peaks of the low order modes of the panel. Thus, this system can effectively reduce both the response and sound radiation at low frequencies where, as discussed in Section 3, passive treatments are less effective. The principal reason why this active system is so effective at low frequencies is because the damping effect produced by the feedback loops is proportional to the absolute transverse velocity of the panel. Thus the so called “sky-hook” active damping effect is produced (Preumont 2002), which effectively reduces the flexural response and sound radiation of the panel. In contrast, the action of a passive damping
treatment is proportional to the strain rate in the structure, which is particularly small at low frequencies where the response is controlled by the lower order modes whose shapes are shown in column (a) of Figure 16. Plots (a) and (b) show that, if the control gains are set to very large values, the response and sound radiation at mid frequencies become even larger than those of the reference panel without control system. This phenomenon is due to the fact that for very large feedback gains, control loops tend to pin the panel at the control positions (Gardonio and Elliott 2005a). Thus the loops do not absorb energy, that is they do not produce active damping anymore. They in fact introduce new boundary conditions, which lead to new set of modes with higher natural frequency. Thus the response and sound radiation of the panel become those of a new, stiffened, panel, with the natural frequencies of the fundamental and low order modes shifted to higher frequencies. As a result, the mid frequency response and sound radiation are increased with respect to those of the reference panel. In conclusion, the 3×3 array of velocity feedback loops produces a very effective sky-hook active damping action which is maximum for a given set of feedback gains. The optimal feedback gains for the minimisation of the response, and thus sound radiation, are very similar to each other (Gardonio and Elliott, 2004). Zilletti et al. (2010) have shown that these correspond to the condition of locally maximising the power absorbed by each feedback loop. This is a very interesting result since it indicates that the feedback loops can be locally tuned without the need of a global cost function to be minimised. Moreover, since the control force is proportional to velocity, the power absorbed given by the product of the control force and control velocity, is in practice proportional to the square of the control velocity. Thus the velocity control sensor signal can be used to implement both the feedback loop and the tuning algorithm necessary to set the optimal control gain.

Plots (c) and (d) in Figure 18 show the kinetic energy PSD and radiated sound power PSD as the control gain of the single feedback loop using a volume velocity distributed sensor and a uniform force distributed actuator is increased. In this case, the control system tends to smoothen the response and sound radiation of selected resonances of the panel. This is because the system can act only on those modes that have a non zero net volumetric component, that is those modes with both mode orders odd. Thus, for example, it cannot be effective on the (1,2), or (2,1) modes, which cause the second and third resonance peaks in the two spectra. However, in this case, since the control system acts on the approximated shape of the first radiation mode, the feedback effect rises indefinitely with the control gain. Thus, provided the control gain is set to large enough values, there is no need of an online tuning system of the control gain. Nevertheless, the control effect produced by this control configuration is relatively lower than that obtained with the decentralised system. It should be highlighted that this result is peculiar to the TBL pressure field primary excitation, which, as discussed in Section 2, effectively excites both volumetric and non volumetric modes.

The short analysis presented in this section about the implementation of active systems for the reduction of vibration and sound radiation by a thin panel excited by a TBL pressure field has been focused on the physics of these control systems. No discussion has been presented on the stability and practical implementation of the feedback loops. This is a very important aspect of the systems, which however lies outside the scope of this chapter. The reader who would like to learn more on this topic is referred to specialised text and articles, as for example those in references (Fuller et al. 1996; Clark et al. 1998; Preumont 2002; Fahy and Gardonio 2007; Gardonio 2012).

3. Acknowledgements

The author is very grateful to Dr Jens Rohlfing and Dr Michele Zilletti for their precious help in the production of simulation graphs and the editing of the text and formulation. Also a special thank goes to Silvia for her support throughout the preparation of the chapter.

[1] d2rp’ d2rp’

c2 dt2 dr2

[3] Identical results are obtained if the analysis is performed in the fixed reference frame if the fixed reference frame cross correlation is obtained by a coordinate transformation from the moving frame as given by Eqn. (22). (See Morris et al. (2002)).

[4]The inclusion of (1 – kM) eliminates the first derivative from the differential operator in the resulting equation.

[5]There are some exceptions to this statement. These cases are described in Section 6.1

[6]ln fact the wave equation can, alternatively, be expressed in terms of a velocity poten­tial, ф, from which density (p = dt), pressure (p = ) and velocity (u = V0) can

all be derived.

[7] In what follows we will see that the flow equations can be manipulated such that this source represents the turbulent jet.

[8]This region is now known to be one of the most important in terms of sound production, but was not known at the time of Lighthill’s first estimates of the sound power radiated by a flow

[9]In 1952 measurement and computational capabilities were such that it was not possible to access full-field data; the two-point correlations were about the best that could be achieved.

[10]The power spectrum is given by taking the Fourier transform

[11]see section 5 for an exposition of POD

[12]This shows that the arbitrary introduction of disturbances to, and subsequent com­parison of, two different analogies cannot provide an unambiguous assessment, in an absolute sense, of the relative robustness of the two formulations. For, if the gradients

[13] Or, stated otherwise, the extent to which that mode is aligned with the propagation operator. If we find that certain modes are not so aligned, this will be an indication that there neglect constitutes a pertinent modelling simplification.

[14]It is true that the LES does not provide a full Navier Stokes solution, being based on filtered equations; we nonetheless consider that it provides a relatively complete rep­resentation of the behaviour of the larger structures, which are those we are interested in here.

[15]In the first study this filter is rather heuristic, being based simply on flow visualisation following the application of Fourier and wavelet transforms; in the second, the filter has a rigorous mathematical definition.

[16]A detalied presentation of LSE is provided in section §5.

[17]The wavelet transform is presented in section §5.

[18]where the pressure is concerned it is, in zone C, predominantly hydrodynamic, while in zone B it contains a increasing proportion of acoustic fluctuation as we move radially away from the jet through zone B

[19] Note that a could comprise both space and time coordinates, and the averaging oper­ation, over b, could be, for example, a phase – or ensemble-average.

[20]In what follows we will drop the the subscript t.

[21]See section §5 for details.

[22]see Noack et al. (2011) for details

[23]The notation evidencing the retarded time is not reported for clarity. Interested readers

in Chapters 1 and 2.

can find a more detailed presentation of this equation and of its theoretical framework

[26] V-n —jn (Junger and Feit 1986).

[27]Ep = ®2Tr[Sqq (Ю)] > (47)

2pc0

where Tr[…] is the trace of the matrix Sqq with the self and mutual PSDs of the acoustic modal responses, which is given by