Adaptive Sparse Grid
Since the function evaluations are very expensive in our application, we introduce in this section an adaptive sparse grid strategy in order to further reduce the number of grid points but conserving the approximation quality. The presented isotropic Smo – lyak algorithm is effective for problems whose input data uniformly depend on all dimensions. But the convergence rate deteriorates for highly anisotropic problems, such as those appearing when the input random variables come from a Karhunen – Loeve-Expansion as in our application [9]. The reduction of computational effort can be achieved by using spatially adaptive or dimension-adaptive refinement [33], [14]. In order to develop adaptive schemes during the cubature process, the interpolation error can be used as an adaptivity indicator. Therefore, nested cubature formulas are useful since they allow the error evaluation based on the difference of two subsequent formulas. Due to the fact that in our application the mean value is computed by the sparse grid interpolation, this target value is also used as an error indicator for the adaptivity. The dimension-adaptive quadrature method tries to find important dimensions and adaptively refines in this with respect to given error estimators. This leads to an approach which is based on generalized sparse grid index sets [14]. This strategy allows to employ every nested interpolation formulas, so it can be chosen problem dependent, e. g. in our application depending on the distribution of the random variables. On the other hand, the locally refined sparse grid gives more flexibility in the adaptive procedure, but requires equidistant support nodes. In the following, we will discuss both strategies and compare the resulting sparse grids in the numerical results later on.
Below, we introduce a locally adaptive hierarchical sparse grid approach using piecewise multilinear hierarchical basis functions following closely [27], [33]. Due to the straightforward implementation of the refinement, we choose the linear hat functions as interpolation basis functions which are also well established in the adaptive mesh refinement. The support nodes of the one-dimensional basis function are given by
with
![]() 1, for і = 1
1, for і = 1
2 і-1 + 1 for і > 1
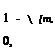 |
 |
||
Hence, the interpolation formulas are defined by
The discussed univariate nodal basis functions (49) are now transformed into multivariate hierarchical basis functions which are fundamental for the adaptive sparse grid. Considering once again the difference formula
f;(h) = Qi+1(h) – Q;(h) (50)
with
Q;(h)= X aj ■ h (Yj) (51)
Y) eGi
we obtain due to the fact that the support nodes are nested (e. g. G; c Gі+1) and accordingly Qі-1 (h) = Q; (Qі-1 (h)) the following representation of (50)
f;(h) = X a) ■ h (y;) – X aj ■ Q)-1 (h) (Y)) (52)
Y’eG Yj eG;
= X a1) ■ (h (y;) – Q)-1 (h) (Yj)) (53)
= X a) ■ (h(Yj) – Q)-1 (h) (Yj)) (54)
Y)G
since h(Y;) – Qi-1(h)(Yj) = 0, yYj e G)-1. Renumbering the elements in Gf = G; Gі-1, with mf = #Gf = m; – m1, leads to
mf
Al(h) = І a) ■ (h(Y)) – Ql-1(h)(Y[)). (55)
j=1
We define wl) = h(Yj) – Q1-1 (h) (y)^ as the 1D hierarchical surplus [6] which is the difference between the current and previous interpolation level. If the 1D Grid of level k interpolates the function h exactly, wk) is equal to zero for all j. So, this value can be used as an error indicator for each inserted grid point, since the hierarchical surpluses tend to zero as the level k tends to infinity (for continuous functions). Considering now again the multi-dimensional case, we obtain the sparse grid (46) in hierarchical form applying the derived formula of A i.
5(k, d)(f)= S(k – 1,d)(f)+ І (Al1 ®-‘®Ald) (f) (56)
|i|=k
= S (k – 1, d)(f ) + AS (k, d)(f) (57)
with
AS(kd)(f)= І І Wn®”’®)) ‘
|i|=*jtBi’—————— V———– ‘
aj
, , , , 44 (58)
(f(^:-’Y)d) -S (k -1d)(f) (и–®))
‘————————- v———————— ‘
wj
where Bi := {j є NN : YІ e G‘A for )l = 1,…, ml&,k = 1,…, d} is a new set of
multi-indices consistent with the multivariate hierarchical basis {aj: j e Bl, l < i}.
Thus, the objective function in our application can be approximated by the following rather abstract expression:
f(P, Wd(Z))= І І wj(p) ■ aj(Z) (59)
|i|<k jeBi
The mean value of the objective function can be then computed as:
en (f (p))= І І wj (p) ■( aj (Wd(Z)) dP (Z) (60)
|i|<k jeBi Jn
where
! f1 ■ l, if l= 1
a) {Y))dY = < •/, if г = 2, (61)
21-1 ■ l, otherwise.
where l denotes the length of the given 1D interval, that means in our example l = 2. Instead of using the hierarchical surplus wij as an error indicator for the adaptivity (cf. [27], [33]), we suggest to adapt the grid checking the following expression:
wj := wj • aj (щ (Q) dP (Z) (62)
Since it is not necessary to exactly interpolate the drag depending on the uncertainty in the optimization loop in our application, the introduced adaptivity indicator wj only measures the difference between the value of the mean inserting a new point Yj of the current level of interpolation and the corresponding value of the mean at the previous interpolation level. The resulting algorithm in order to construct the sparse grid which is then used for the optimization slightly differs from [27], [33] due to the modification in the adaptivity indicator.











