Derivation of the coupled structural-acoustic response
In general, for the structural-acoustic problem at hand, the shell structure is excited only by transverse force distributions. For instance, for the cylindrical wall of the model problem shown in Figure 1, the excitation vector is characterised only by forces in radial direction. More specifically, the transverse force excitation per unit surface fr (x’s) is composed by three terms: the pressure
field prai(x’s, t) produced by the TBL fluid flow and the fluid loading pressure fields pe (xs, t), pc (xs, t) exerted by the external and internal fluids.
As discussed in the opening part of this section, the pressure field produced by the TBL fluid flow is assumed independent from the flexural vibration of the cylindrical shell. In this case the excitation is specified in terms of the blocked pressure. Comprehensive overviews of the models for the excitation spectra that have been proposed since the early work by Corcos (1963a); (Corcos 1963b) can be found in Bull (1995); Graham (1997) and in Chapter 6 of this book. In this respect, it is important to emphasize that, despite the growing evidence that the model proposed by Corcos (Corcos 1963a; Corcos 1963b; Corcos 1967) over predicts the excitation levels at wavenumbers below the convective coincidence range (Martin and Leehey 1977; Blake 1986; Leehey 1988), it is still widely used to predict the response and interior sound radiation in high speed transportation vehicles such as aircraft. This is because, for high flow speeds, the convective coincidence range tends to coincide with the wavenumbers of the low order natural modes of the shell structure controlling the response and interior sound radiation phenomena (Graham 1997; Cousin 1999; Maury et al. 2002b). Nevertheless it is important to highlight that situations exist where the contribution in the sub-convective wavenumber region may be significant (Hwang and Maidanik 1990; Graham 1997).
The external and internal fluid loadings are instead derived considering the feedback effects produced by the flexible wall sound radiation into the external and internal fluids. As anticipated at the beginning of this section, this is a reasonable model for the fluid loadings produced by the air in the interior and exterior of a vehicle that travels at low speed. For aircraft vehicles traveling at very high speed approaching 0.8 Mach at cruise condition, a proper aeroelastic formulation would be necessary to correctly predict the exterior fluid loading (Frampton 2005). Nonetheless, the structural-acoustic model presented here provides a good foundation for the understanding of the physical mechanisms characterising the coupling of structural modes via the internal and external fluids. In this respect, a complete set of graphs with the spectra of the self and mutual fluid loading impedance functions is introduced at the end of this subsection, which provide direct indications on the damping-, mass – and
![]()
stiffness-like physical effects produced between the modes of the shell via the fluid loading.
In summary, the excitation exerted by the TBL fluid flow on the wall structure is expressed in terms of the blocked TBL pressure pTBL (x’s), which is twice the pressure that a nominally identical flow would produce if the wall was removed (Howe 1998). Also, the exterior and interior sound pressure fields, pe(xs, t) and pc(xs, t), are derived from the first step “collocation analysis” of the boundary integral in Eq. (5). As discussed above, if there are no distributions of acoustic sources in the exterior and interior fluid domains, the boundary integral expression (5) reduces to Eq. (11) and Eq. (19) when both the exterior and interior sound fields are described with Neumann Green functions. For instance, assuming that the acoustic particle velocity on the boundary surface of the model problem shown in Figure 1 coincides with the radial velocity of the cylinder, i. e. Vn (xs)=w(xs), the radial force per unit surface is given by4
Since the natural modes used to derive the structural response are characterised by the symmetric and anti-symmetric functions given in Eqs. (28a, b), the modal excitation terms defined in Eq. (30) are expressed as follows
![]() f“m = Фг, т (X’s)PTBL (x’s )dSb “ 2,ь Фг, т j^PGe (< xs )w(xs )dS4dS4
f“m = Фг, т (X’s)PTBL (x’s )dSb “ 2,ь Фг, т j^PGe (< xs )w(xs )dS4dS4
– 2£ Фг, т j®fGc (x’s Xs )W(Xs )dSbdSb
Here, the two Green functions Ge and Gc are given by Eqs. (13) and (22) respectively. Thus, considering the orthonormal properties of the trigonometric functions that describe the structural and acoustic mode shapes and the Green functions for the external fluid domain, simplified analytical expressions can be derived for the three integrals in the equation above. In particular, the first integral is expressed in terms of TBL modal excitations while, considering the modal expansion for the radial displacement given by Eq. (26), the other two integrals are expressed in the form of modal impedances. Thus it follows that:
Here the TBL modal excitations are given by
Also, the modal impedance terms due to the interaction between the modal vibration of the cylinder wall and exterior fluid are given by (Junger and Feit 1986; Lesueur 1988)
where Nmhml(kz)=icos2(jkr) when m and m are odd while Nm,,mi(kz)=-2sin2(k|L-) when m1 and m1 are even. In addition km = , k – = and є-2=0 = 1,
emi>0 = 2 is the Neumann factor. Finally (Junger and Feit 1986; Lesueur 1988)
is an impedance function per unit surface, where, as introduced in Section 1.2, k2 = k2 + k2 and H(m)(…) is the first kind Hankel function of order m,. Since the flexural natural modes of the cylinder are orthogonal to each other, no coupling exists, i. e. Z“mm = 0 , when m + m is odd or when m2 Ф m2. Finally, the modal
impedance terms due to the interaction between the cylinder wall and interior fluid are given by
where the mode coupling terms are given by (Gardonio et al. 2001)
with esni = 1 when n2 = 0 and єsr2 = 2 when n2 ф 0 and with earh= 2 for all n2. Also in this case, the orthonormal properties of the trigonometric functions in the natural modes leads to no coupling, i. e. Zacmm = 0, between modes with m — n1,n + 2, n + 4, … or m — n1,n + 2, n + 4, … and m2 Фn2 or m2 Фn2.
Substitution of Eq. (35) into Eq. (29) gives the following set of coupled modal equations
-®2)k_ = fraEL, m – jv t – jv tКЖт
![]() m=1 m=1
m=1 m=1
a=s, a a=s, a
m = 1, 2, …. x a = s, a
To simplify the remaining part of the formulation, these equations are arranged in the following matrix expression
[- ®2M + jdL + K]br = frBL , (42)
where the elements of the diagonal mass and stiffness matrices are given by M = M and K“ = Matm respectively. Also, the elements of the modal
excitation and modal response vectors are given by f“BLm = fBBLm and b“m = barm respectively. Finally the complex terms in the sparse impedance matrix are given by Z“_ ^(z“mm + Z“mm).The diagonal self impedance terms provide the exterior and interior fluid loading effects on a given mode m = (m1, m2) exerted by the modal velocity of the same mode m = (m1, m2). Alternatively the off-diagonal mutual impedance terms (often called cross impedances) give the exterior and interior fluid loading effects on a given mode m = (m1, m2) generated by the modal velocity of another mode m – (m1,m2).
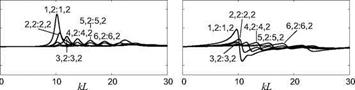
Before continuing with the final part of this formulation for the interior sound radiation, the physical effects due to the fluid loadings produced by the external and internal air fluids are studied in detail for a cylindrical enclosure with aspect ratio RL=03. To facilitate the analysis, the spectra with the real and imaginary parts of the self and mutual impedances given in Eqs. (37) and (39) are presented. The fluid loading effects are then analysed recalling that a) a real positive impedance indicates a damping-like effect, i. e. Zdamping = c; b) an
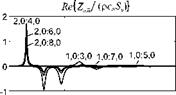
imaginary positive impedance proportional to frequency denotes a mass-like effect, i. e. Zmass – jam; and c) a imaginary negative impedance inversely proportional to frequency indicates a stiffness-like effect, i. e. Zstifjness = – jk/ m (here c, m, k, represent the damping, mass and stiffness factors respectively). Figure 3 shows the spectra of the real (left-hand side plots) and imaginary (right-hand side plots) parts of normalised self modal impedances of a cylinder immerged in air. The three rows of graphs show the self modal impedances with circumferential mode numbers m2 = 0, 1, 2 . The left-hand side plots shows that
the spectra of the real parts are always positive. This indicates that the fluid produces a resistive effect on each mode, thus it absorbs energy from the modal vibrations of the cylinder. In general, at low frequencies, all spectra set off from
![]()
 |
|||
|
|||
|
|||
|
|
||
|
|||
|
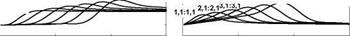



very small values close to zero and then rapidly rise up to a maximum value in correspondence of specific critical frequencies <z>cnmm. Above these critical
frequencies, the resistive effects rapidly fall and then level to constant values of 0.5 for the breathing modes with m2 = 0 and 0.25 for the other modes with m2 > 0 . Thus, in general, the self modal loading exerted by the external fluid
produces large resistive effects at high frequencies starting from about the modal critical frequencies where the resistive effect is maximum. Also, the resistive effects produced by breathing modes are double than those of modes with higher circumferential mode orders. Finally the critical frequencies rise together with the axial mode orders m1 = m1. Moving to the right-hand side plots, it is noted that also the spectra for the imaginary parts are always positive, which indicates that the fluid also produces a mass effect on each mode. In general, all spectra grow rapidly from zero and reach a maximum value at frequencies slightly lower than the modal critical frequency &>cr, mm. Then, for higher frequencies, they
rapidly fall to zero. Thus, in general, the self modal loading exerted by the external fluid produces mass effects up to the critical frequencies. Also, the peak mass effects produced by breathing modes are double than those of modes with higher circumferential mode orders.
Figure 4 shows the spectra of the real part (left-hand side plots) and imaginary part (right-hand side plots) of normalised mutual modal impedances with circumferential mode numbers m2 = 0, 1, 2 . The two columns of graphs show
that in this case the real and the imaginary parts assume both positive and negative values. This indicates that the fluid tends to transfer energy between pairs of modes. In general, the spectra for both the real and imaginary parts start from zero and then depict a waved contour that peaks at frequencies below the upper critical frequency of the two modes and then rapidly fade to zero. Thus, in general, the mutual fluid loading effect transfers energy from one mode to another around the upper critical frequencies o)crmm of the two modes. Plots in Figure 4 highlight that this effect is larger for breeding modes with m2 = 0 and
progressively becomes smaller as the circumferential mode order grows. In general, as can be noted by contrasting the graphs in Figures 3 and 4, for light fluids the energy transfer between pairs of modes is much smaller than the energy absorption exerted on single modes (Guyader and Laulagnet 1994). For this reason, the effect of the mutual impedances is often neglected for light fluids, such as air for example, so that the set of equations (41) becomes uncoupled. To conclude this analysis, it is important to note that, according to Eq. (37) and (38), the modal impedance terms relative to the external fluid loading are proportional to the specific acoustic impedance of the fluid pc0.
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|
|
|||
|
![]()

Thus the energy absorption and transfer effects, as well as the mass effects described above, become increasingly important for heavy fluids (e. g. water). Normally, for light fluids, such as air, the mutual fluid loading effects and the self mass fluid loading effects are neglected. Also, the self resistive effects are described in terms of a viscous damping ratio, which is often considered constant and equal for all modes, although it should follow the typical spectra shown in the left-hand side plots of Figure 3.
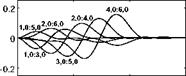
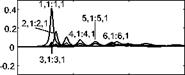
The modal impedance effects produced by the interior fluid is now analysed assuming the cylinder is filled with air and has aspect ratio RL=03. Figure 5
shows the spectra of the real (left-hand side plots) and imaginary (right-hand side plots) parts of the normalised self modal impedances with circumferential mode numbers m2 = 0, 1, 2 . The left-hand side plots show that the spectra of the real parts are positive and are characterised by peaks occurring at the resonance frequencies relative to acoustic modes that are efficiently coupled with the structural mode that specifies the modal impedance term. The right-hand side plots show that the spectra of the imaginary parts jump from positive to negative values in correspondence of these resonances. Thus, the interior fluid produces a combination of stiffness, dissipative and mass effects on single structural modes, which is typical of enclosed sound fields with resonant behaviour (Kinsler et al. 2000). More specifically the stiffness effect is produced at frequencies below resonance while the mass effect is generated at frequencies above resonance. Also, the dissipative effect becomes significant at frequencies around resonance. On average, the magnitude of the impedances for breathing modes with circumferential mode order m2 = 0 is one order of magnitude greater than that of modes with higher circumferential mode orders. Also, for a given circumferential mode order, the magnitude of the resonance peaks tends to decrease as the axial mode number m1 rises. Finally, the modal impedances of breathing modes are characterised by a low frequency stiffness behaviour, which is due to the elastic reaction offered by the fluid in the cavity to the volumetric modal vibration.
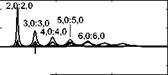
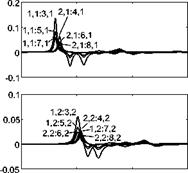
Figure 6 shows the real part (left-hand side plots) and the imaginary part (right-hand side plots) of the normalised mutual modal impedances with circumferential mode numbers m2 = 0, 1, 2 . The left-hand side plots show that the
spectra for the real parts of the mutual modal impedances are also characterised by peaks occurring at the resonance frequencies due to the acoustic modes that are efficiently coupled with the structural mode that specifies the modal impedances. However, in this case, the peaks assume either positive or negative values. As found for the self impedances, the right-hand side plots show that the spectra for the imaginary parts are characterised by a discontinuity in correspondence of the resonance frequencies where the co-respective real part
peaks. However, in this case the jumps can be either from negative to positive values or from positive to negative values. Thus, the interior fluid produces a combination of stiffness, dissipative and mass effects also between pairs of structural modes, although the order of the stiffness and mass effects is inverted for certain pairs of structural modes. This phenomenon is indicative of an energy transfer between pairs of modes. Similarly to the self impedance functions shown in Figure 5, the average magnitude of the impedances for breathing modes with circumferential mode order m2 = 0 is much larger than that of modes with higher circumferential mode orders. Also, for a given circumferential mode order, the average magnitude tends to decrease as the axial mode number m1 rises. Finally, as seen for the modal impedances produced by the external fluid, Eqs. (39) and (40) indicate that the modal impedance is proportional to the specific acoustic impedance of the fluid pc0. Thus the energy absorption and transfer effects as well as the mass effects become increasingly important for heavy fluids, e. g. water. In general, for light fluids such as air, the mutual fluid loading is neglected and the self fluid loading is assumed purely dissipative. In this way, as seen for the modal impedances exerted by the exterior fluid, the self dissipative effects are described in terms of a viscous damping ratio, which is often considered constant and equal for all modes, although it should comply with the typical spectra shown in the left-hand side plots of Figure 5.