Dimension Adaptive Sparse Grid
The main advantage of the dimension adaptive refinement strategy is the fact that one can use problem dependent quadrature formulas in order to construct the adaptive sparse grid. In our application, the objective function, the drag, is multiplied by the Gaussian density function, so that Gaussian Hermite polynomials are optimal with respect to the weighting function.
First, a generalization of sparse grids will be introduced which allows to weight the dimensions according to their importance on the target functional. The idea of generalized sparse grids and especially dimension adaptive sparse grid can be found in [14], [12], [7] and [26]. The original sparse grid of order k combines all the incremental functions which sum up to order k, that means only those indices are considered which are contained in the unit simplex |i| < k. [14] and [13] suggest to allow a more general index set which can be then adaptively chosen with respect to the importance of each dimension.
An index set I is called admissible if Vi є I
i – ej є I, V1 < j < d, kj > 1,
where ej є Rd is the jth unit vector. The generalized index set I contains for an index i all indices which have smaller entries in one or more dimensions. Due to this fact, the incremental sparse grid formula (46) is still well defined for the new index sets and is given as
5(k, d)(f)= X (4і1 ^•••сзА) (f). (63)
іє!
The generalized definition of sparse grids includes the original sparse grid and the full tensor grid definition (cf. (46), (43)). Further, equation (63) particularly leaves more flexibility to the choice of the grids and therefore allows to handle anisotropic problems which emphasize the following example of an admissible index set in R2:
|
|
This example of an admissible index set i shows the feasibility of an refinement in only one dimension (here in the first dimension) which is the required feature for the adaptivity.
If a priori knowledge of the underlying function is available, an admissible index set with respect to the additional information can be chosen. Since this is not the case in our application, an algorithm is introduced in the following which automatically computes an admissible index set in a dimension adaptive way (cf. [14], [13]). Therefor, we start with the coarsest sparse grid, that means I = {(0,.. .,0)} and successively add new indices such that
• the new index set remains admissible
• the approximation error is reduced.
For the second point, an error indicator is needed. Taking a look at the difference formula (63), the term
A i = (A ®—®Aid) (f) (64)
indicates the reduction in the approximated integral for each new added index. [14] suggests to further involve the number of function evaluations to avoid an too early stopping. Since equation (64) shows good results in our application, we directly use Ai as an error indicator for the adaptivity.
As mentioned before, the main advantage of the dimension adaptive refinement is the fact that the quadrature formulas can be chosen problem dependent. Considering geometry uncertainties in the robust optimization, the Karhunen-Loeve expansion leads to the following objective function
E (f (y, p, W(x, Q’Y) = ■■■ (f (y, p, Wd (x, Y1(Q,…,Yd (С))Мф1(Z) (Z),
n n
so that the Gaufi-Hermite formulas are an appropriate choice for the quadrature. The one dimensional Hermite polynomials are orthogonal polynomials over (-o, o) with the weight function <n(x) = exp(-x2). The Gaufi-Hermite quadrature belongs to the class of Gaufiformulas which are constructed by choosing both the points and the weights with the goal to exactly integrate as many polynomials as possible. The Gaufiformulas achieve the polynomial exactness of 2n – 1 where n is the number of abscissas of the quadrature rule. In GaufiHermite quadrature the integral of the form f-oo f (x) exp(-x2)dx is approximated by
f(x)exp(-x2)dx « £ a>if (xi) (65)
i=1
where the abscissas xi are zeros of the mth Hermite polynomial and the coi are the corresponding weights. The Hermite polynomials are defined as
dn
H„(x) = (-l)"exp(.r) — exp(-.r) (66)
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
 |
|
|
|
|
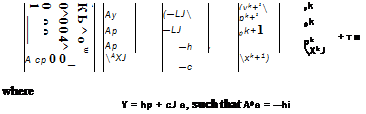
(1) generate hk by performing N iterations of an adjoint solver with right hand side fj (yk, pk) starting in hk
(2) generate ak by performing N iterations of an adjoint solver with right hand side hj (yk, pk) starting in ak
(3) compute approximate reduced gradients
g = fj + cjhk+1, y = hj + cp ak+1
(4) generate Bk+1 as an approximation of the (consistent) reduced Hessian
(5) solve the QP
B y]( &p = (-g Yj 0 pk+1 – h
(6) update pk+1 = pk + Ap
(7) compute the corresponding geometry and adjust the computational mesh
(8) generate yk+1 by performing N iterations of the forward state solver starting from an interpolation of yk at the new mesh.
This highly modular algorithmic approach is not an exact transcription of equation (69), but is shown in [16] to be asymptotically equivalent and to converge to the same solution. The overall algorithmic effort for this algorithm is typically in the range of factor 7 to 10 compared to a forward stationary simulation.
Now we generalize this algorithmic framework to the semi-infinite problem formulation (23-25). Numerical approaches to this problem class have already been proposed in [2, 3, 4].
For the sake of simplicity, we restricted the formulation to a problem with two set-points coupled via the objective, which is a weighted sum of all set-point objectives (weights: ю1, (o2), and via the free optimization variables p, which are the same for all set-points. The generalization to more setpoints (i. e., the adaptive sparse grid points below) is then obvious. The lift constraint is formulated for the smallest value smin of all grid points. The corresponding Lagrangian in our example is
2 2
L (У1, У2, p, h,h) = Zfi, p, ^) + p, si )+ph(ymin, p, smin) (70)
i=1 i=1
The approximate reduced SQP method above applied to this case can be written in the following form
|
О о о о о |
Ay1^ |
(-LA |
||
|
0 0 0 0 0 Aj |
Ay2 |
-к |
||
|
00 B y cjp cj, p |
Ap |
-Lj |
||
|
О о о Г*" о о |
Ар |
-h |
||
|
о о о о. о о |
Ah |
-c1 |
||
|
0 A2 c2,p 0 0 0 |
уАА2 |
-c2 |
We notice that the linear sub-problems involving matrices Aj are to be solved independently, and therefore trivially in parallel. The information from all these parallel adjoint problems is collected in the reduced gradient
2 2
g = + Ecj
i=1 i=1
Next, the solution of optimization step
"B n]( ap = f-g
Yj 0 pk+1) -hJ
is distributed to all approximate linearized forward problems
AiAyi + Ci, pAp = – Ci,
which can then again be performed in parallel.











